Schlagwort: Other

Schlagwortarchiv für: Other

Secret Sharing DAOs: The Other Crypto 2.0

The crypto 2.0 industry has been making strong progress in the past year developing blockchain technology, including the formalization and in some cases realization of proof of stake designs like Slasher and DPOS, various forms of scalable blockchain algorithms, blockchains using “leader-free consensus” mechanisms derived from traditional Byzantine fault tolerance theory, as well as economic ingredients like Schelling consensus schemes and stable currencies. All of these technologies remedy key deficiencies of the blockchain design with respect to centralized servers: scalability knocks down size limits and transaction costs, leader-free consensus reduces many forms of exploitability, stronger PoS consensus algorithms reduce consensus costs and improve security, and Schelling consensus allows blockchains to be “aware” of real-world data. However, there is one piece of the puzzle that all approaches so far have not yet managed to crack: privacy.

Currency, Dapps and Privacy

Bitcoin brings to its users a rather unique set of tradeoffs with respect to financial privacy. Although Bitcoin does a substantially better job than any system that came before it at protecting the physical identities behind each of its accounts – better than fiat and banking infrastructure because it requires no identity registration, and better than cash because it can be combined with Tor to completely hide physical location, the presence of the Bitcoin blockchain means that the actual transactions made by the accounts are more public than ever – neither the US government, nor China, nor the thirteen year old hacker down the street even need so much as a warrant in order to determine exactly which account sent how much BTC to which destination at what particular time. In general, these two forces pull Bitcoin in opposite directions, and it is not entirely clear which one dominates.

With Ethereum, the situation is similar in theory, but in practice it is rather different. Bitcoin is a blockchain intended for currency, and currency is inherently a very fungible thing. There exist techniques like merge avoidance which allow users to essentially pretend to be 100 separate accounts, with their wallet managing the separation in the background. Coinjoin can be used to “mix” funds in a decentralized way, and centralized mixers are a good option too especially if one chains many of them together. Ethereum, on the other hand, is intended to store intermediate state of any kind of processes or relationships, and unfortunately it is the case that many processes or relationships that are substantially more complex than money are inherently “account-based”, and large costs would be incurred by trying to obfuscate one’s activities via multiple accounts. Hence, Ethereum, as it stands today, will in many cases inherit the transparency side of blockchain technology much more so than the privacy side (although those interested in using Ethereum for currency can certainly build higher-privacy cash protocols inside of subcurrencies).

Now, the question is, what if there are cases where people really want privacy, but a Diaspora-style self-hosting-based solution or a Zerocash-style zero-knowledge-proof strategy is for whatever reason impossible – for example, because we want to perform calculations that involve aggregating multiple users’ private data? Even if we solve scalability and blockchain data assets, will the lack of privacy inherent to blockchains mean that we simply have to go back to trusting centralized servers? Or can we come up with a protocol that offers the best of both worlds: a blockchain-like system which offers decentralized control not just over the right to update the state, but even over the right to access the information at all?

As it turns out, such a system is well within the realm of possibility, and was even conceptualized by Nick Szabo in 1998 under the moniker of “God protocols” (though, as Nick Szabo pointed out, we should not use that term for the protocols that we are about to describe here as God is generally assumed or even defined to be Pareto-superior to everything else and as we’ll soon see these protocols are very far from that); but now with the advent of Bitcoin-style cryptoeconomic technology the development of such a protocol may for the first time actually be viable. What is this protocol? To give it a reasonably technically accurate but still understandable term, we’ll call it a “secret sharing DAO”.

Fundamentals: Secret Sharing

Secret computation networks rely on two fundamental primitives to store information in a decentralized way. The first is secret sharing. Secret sharing essentially allows data to be stored in a decentralized way across N parties such that any K parties can work together to reconstruct the data, but K-1 parties cannot recover any information at all. N and K can be set to any values desired; all it takes is a few simple parameter tweaks in the algorithm.

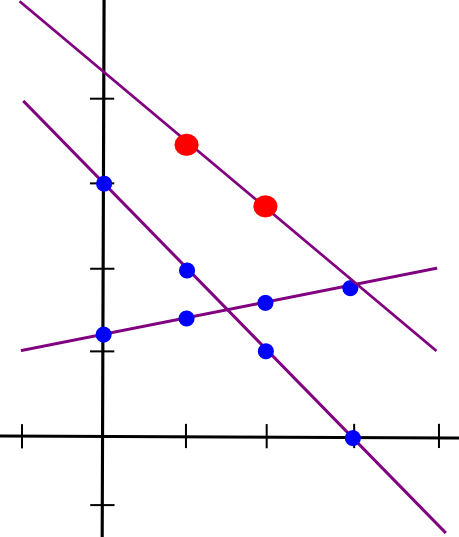
The simplest way to mathematically describe secret sharing is as follows. We know that two points make a line:

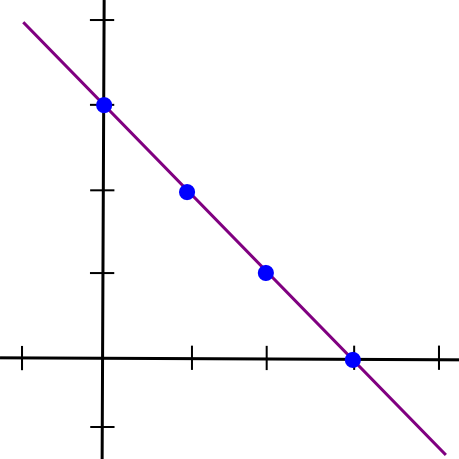
So, to implement 2-of-N secret sharing, we take our secret S, generate a random slope m, and create the line y = mx + S. We then give the N parties the points on the line (1, m + S), (2, 2m + S), (3, 3m + S), etc. Any two of them can reconstruct the line and recover the original secret, but one person can do nothing; if you receive the point (4, 12), that could be from the line y = 2x + 4, or y = -10x + 52, or y = 305445x - 1221768. To implement 3-of-N secret sharing, we just make a parabola instead, and give people points on the parabola:

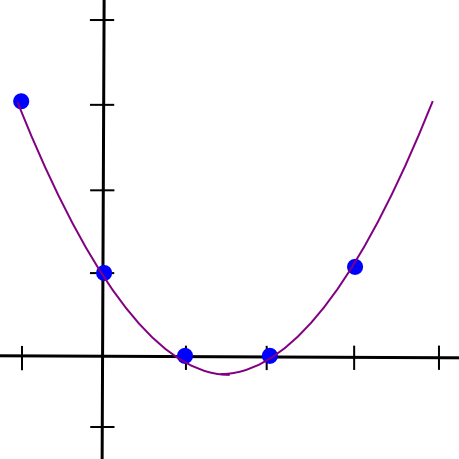
Parabolas have the property that any three points on a parabola can be used to reconstruct the parabola (and no one or two points suffice), so essentially the same process applies. And, more generally, to implement K-of-N secret sharing, we use a degree K-1 polynomial in the same way. There is a set of algorithms for recovering the polynomial from a sufficient set of points in all such cases; they are described in more details in our earlier article on erasure coding.

This is how the secret sharing DAO will store data. Instead of every participating node in the consensus storing a copy of the full system state, every participating node in the consensus will store a set of shares of the state – points on polynomials, one point on a different polynomial for each variable that makes up part of the state.

Fundamentals: Computation

Now, how does the secret sharing DAO do computation? For this, we use a set of algorithms called secure multiparty computation (SMPC). The basic principle behind SMPC is that there exist ways to take data which is split among N parties using secret sharing, perform computations on it in a decentralized way, and end up with the result secret-shared between the parties, all without ever reconstituting any of the data on a single device.

SMPC with addition is easy. To see how, let’s go back to the two-points-make-a-line example, but now let’s have two lines:

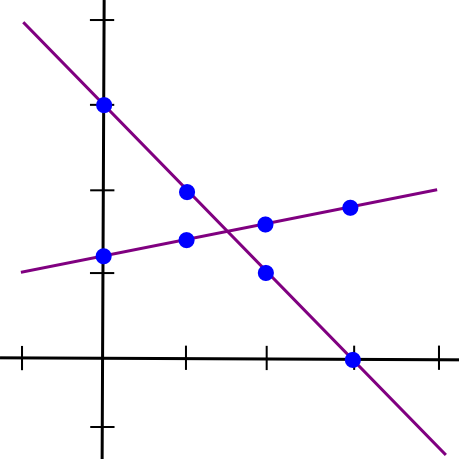
Suppose that the x=1 point of both lines A and B is stored by computer P[1], the x=2 point is stored by computer P[2], etc. Now, suppose that P[1] computes a new value, C(1) = A(1) + B(1), and B computes C(2) = A(2) + B(2). Now, let’s draw a line through those two points:

So we have a new line, C, such that C = A + B at points x=1 and x=2. However, the interesting thing is, this new line is actually equal to A + B on every point:

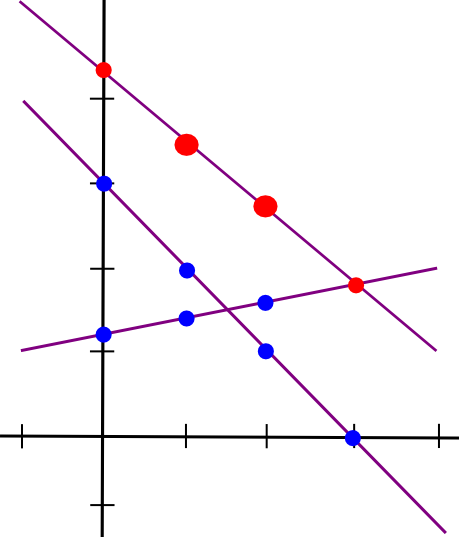
Thus, we have a rule: sums of secret shares (at the same x coordinate) are secret shares of the sum. Using this principle (which also applies to higher dimensions), we can convert secret shares of a and secret shares of b into secret shares of a+b, all without ever reconstituting a and b themselves. Multiplication by a known constant value works the same way: k times the ith secret share of a is equal to the ith secret share of a*k.

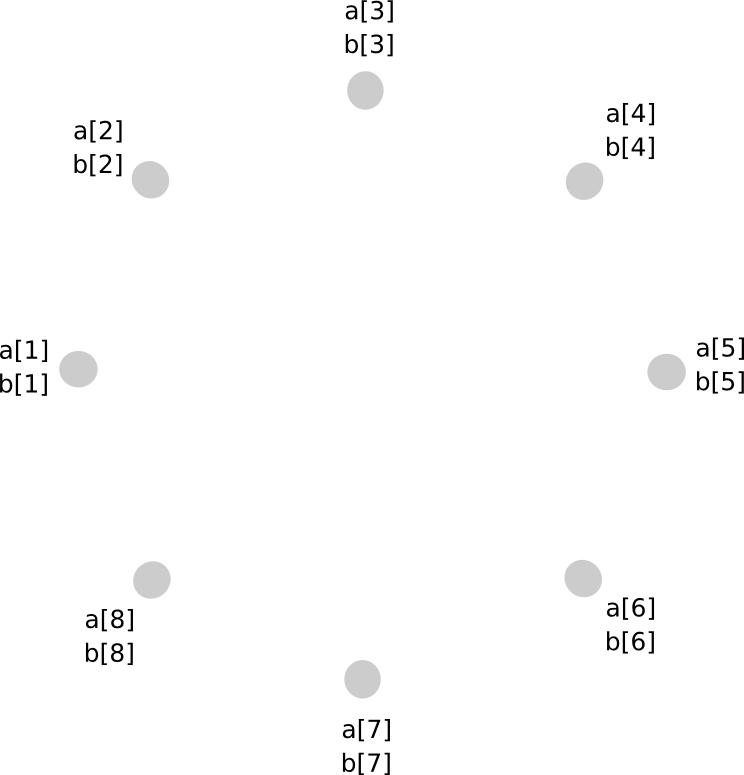
Multiplication of two secret shared values, unfortunately, is much more involved. The approach will take several steps to explain, and because it is fairly complicated in any case it’s worth simply doing for arbitrary polynomials right away. Here’s the magic. First, suppose that there exist values a and b, secret shared among parties P[1] … P[n], where a[i] represents the ith share of a (and same for b[i] and b). We start off like this:

Now, one option that you might think of is, if we can just make a new polynomial c = a + b by having every party store c[i] = a[i] + b[i], can’t we do the same for multiplication as well? The answer is, surprisingly, yes, but with a serious problem: the new polynomial has a degree twice as large as the original. For example, if the original polynomials were y = x + 5 and y = 2x - 3, the product would be y = 2x^2 + 7x - 15. Hence, if we do multiplication more than once, the polynomial would become too big for the group of N to store.

To avoid this problem, we perform a sort of rebasing protocol where we convert the shares of the larger polynomial into shares of a polynomial of the original degree. The way it works is as follows. First, party P[i] generates a new random polynomial, of the same degree as a and b, which evaluates to c[i] = a[i]*b[i] at zero, and distributes points along that polynomial (ie. shares of c[i]) to all parties.

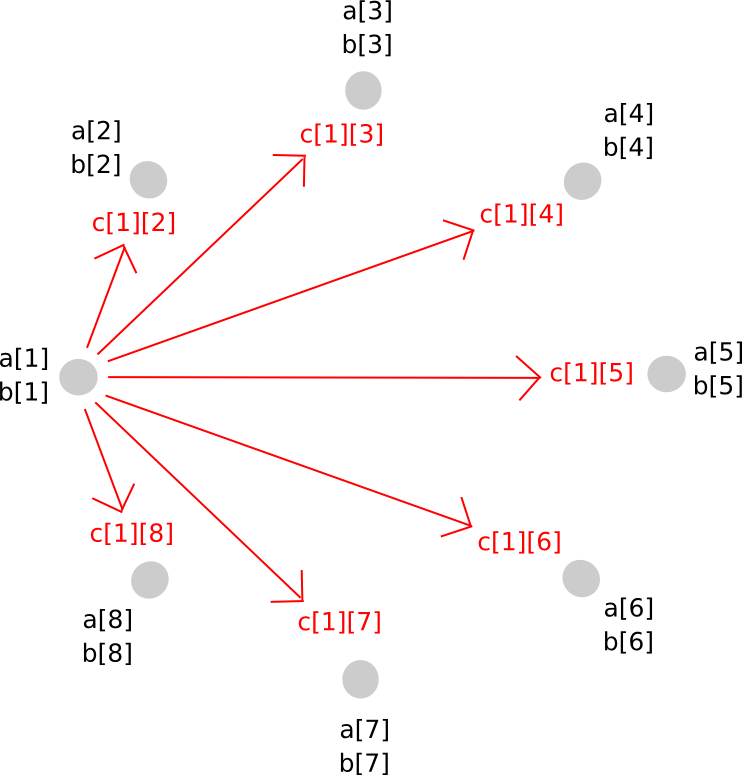
Thus, P[j] now has c[i][j] for all i. Given this, P[j] calculates c[j], and so everyone has secret shares of c, on a polynomial with the same degree as a and b.

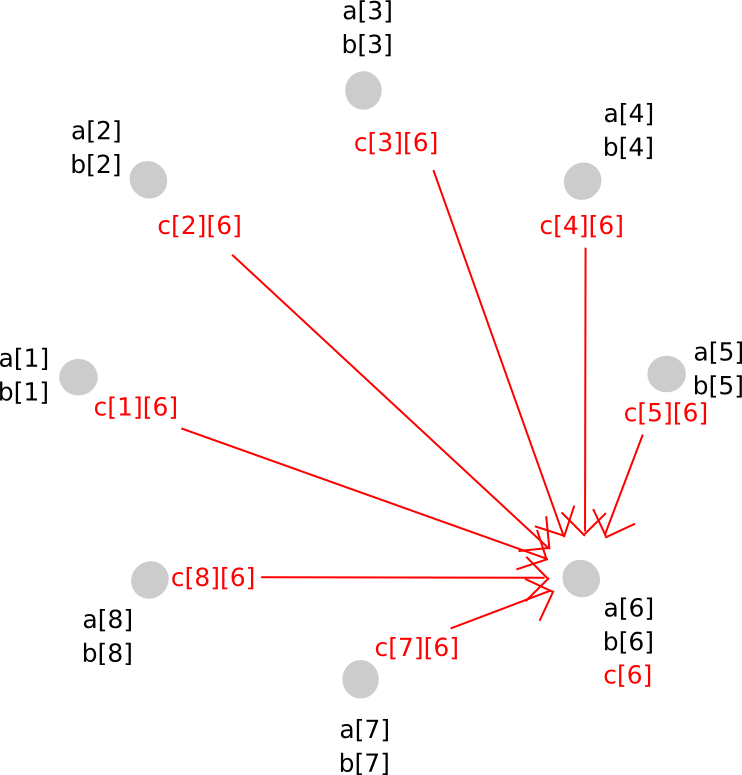
To do this, we used a clever trick of secret sharing: because the secret sharing math itself involves nothing more than additions and multiplications by known constants, the two layers of secret sharing are commutative: if we apply secret sharing layer A and then layer B, then we can take layer A off first and still be protected by layer B. This allows us to move from a higher-degree polynomial to a lower degree polynomial but avoid revealing the values in the middle – instead, the middle step involved both layers being applied at the same time.

With addition and multiplication over 0 and 1, we have the ability to run arbitrary circuits inside of the SMPC mechanism. We can define:

AND(a, b) = a * b
OR(a, b) = a + b - a * b
XOR(a, b) = a * b - 2 * a * b
NOT(a) = 1 - a

Hence, we can run whatever programs we want, although with one key limitation: we can’t do secret conditional branching. That is, if we had a computation if (x == 5) <do A> else <do B> then the nodes would need to know whether they are computing branch A or branch B, so we would need to reveal x midway through.

There are two ways around this problem. First, we can use multiplication as a “poor man’s if” – replace something like if (x == 5) <y = 7> with y = (x == 5) * 7 + (x != 5) * y, using either circuits or clever protocols that implement equality checking through repeated multiplication (eg. if we are in a finite field we can check if a == b by using Fermat’s little theorem on a-b). Second, as we will see, if we implement if statements inside the EVM, and run the EVM inside SMPC, then we can resolve the problem, leaking only the information of how many steps the EVM took before computation exited (and if we really care, we can reduce the information leakage further, eg. round the number of steps to the nearest power of two, at some cost to efficiency).

The secret-sharing based protocol described above is only one way to do relatively simply SMPC; there are other approaches, and to achieve security there is also a need to add a verifiable secret sharing layer on top, but that is beyond the scope of this article – the above description is simply meant to show how a minimal implementation is possible.

Building a Currency

Now that we have a rough idea of how SMPC works, how would we use it to build a decentralized currency engine? The general way that a blockchain is usually described in this blog is as a system that maintains a state, S, accepts transactions, agrees on which transactions should be processed at a given time and computes a state transition function APPLY(S, TX) -> S' OR INVALID. Here, we will say that all transactions are valid, and if a transaction TX is invalid then we simply have APPLY(S, TX) = S.

Now, since the blockchain is not transparent, we might expect the need for two kinds of transactions that users can send into the SMPC: get requests, asking for some specific information about an account in the current state, and update requests, containing transactions to apply onto the state. We’ll implement the rule that each account can only ask for balance and nonce information about itself, and can withdraw only from itself. We define the two types of requests as follows:

SEND: [from_pubkey, from_id, to, value, nonce, sig] GET: [from_pubkey, from_id, sig]

The database is stored among the N nodes in the following format:

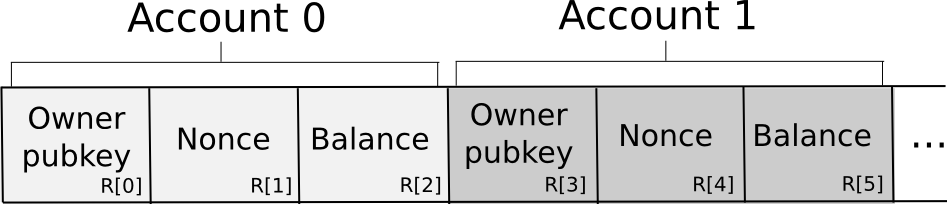
Essentially, the database is stored as a set of 3-tuples representing accounts, where each 3-tuple stores the owning pubkey, nonce and balance. To send a request, a node constructs the transaction, splits it off into secret shares, generates a random request ID and attaches the ID and a small amount of proof of work to each share. The proof of work is there because some anti-spam mechanism is necessary, and because account balances are private there is no way if the sending account has enough funds to pay a transaction fee. The nodes then independently verify the shares of the signature against the share of the public key supplied in the transaction (there are signature algorithms that allow you to do this kind of per-share verification; Schnorr signatures are one major category). If a given node sees an invalid share (due to proof of work or the signature), it rejects it; otherwise, it accepts it.

Transactions that are accepted are not processed immediately, much like in a blockchain architecture; at first, they are kept in a memory pool. At the end of every 12 seconds, we use some consensus algorithm – it could be something simple, like a random node from the N deciding as a dictator, or an advanced neo-BFT algorithm like that used by Pebble – to agree on which set of request IDs to process and in which order (for simplicity, simple alphabetical order will probably suffice).

Now, to fufill a GET request, the SMPC will compute and reconstitute the output of the following computation:

owner_pubkey = R[0] * (from_id == 0) + R[3] * (from_id == 1) + ... + R[3*n] * (from_id == n)  valid = (owner_pubkey == from_pubkey)  output = valid * (R[2] * (from_id == 0) + R[5] * (from_id == 1) + ... + R[3n + 2] * (from_id == n))

So what does this formula do? It consists of three stages. First, we extract the owner pubkey of the account that the request is trying to get the balance of. Because the computation is done inside of an SMPC, and so no node actually knows what database index to access, we do this by simply taking all the database indices, multiplying the irrelevant ones by zero and taking the sum. Then, we check if the request is trying to get data from an account which is actually owns (remember that we checked the validity of from_pubkey against the signature in the first step, so here we just need to check the account ID against the from_pubkey). Finally, we use the same database getting primitive to get the balance, and multiply the balance by the validity to get the result (ie. invalid requests return a balance of 0, valid ones return the actual balance).

Now, let’s look at the execution of a SEND. First, we compute the validity predicate, consisting of checking that (1) the public key of the targeted account is correct, (2) the nonce is correct, and (3) the account has enough funds to send. Note that to do this we once again need to use the “multiply by an equality check and add” protocol, but for brevity we will abbreviate R[0] * (x == 0) + R[3] * (x == 1) + ... with R[x * 3].

valid = (R[from_id * 3] == from_pubkey) * (R[from_id * 3 + 1] == nonce) * (R[from_id * 3 + 2] >= value)

We then do:

R[from_id * 3 + 2] -= value * valid R[from_id * 3 + 1] += valid R[to * 3 + 2] += value * valid

For updating the database, R[x * 3] += y expands to the set of instructions R[0] += y * (x == 0), R[3] += y * (x == 1) .... Note that all of these can be parallelized. Also, note that to implement balance checking we used the >= operator. This is once again trivial using boolean logic gates, but even if we use a finite field for efficiency there do exist some clever tricks for performing the check using nothing but additions and multiplications.

In all of the above we saw two fundamental limitations in efficiency in the SMPC architecture. First, reading and writing to a database has an O(n) cost as you pretty much have to read and write every cell. Doing anything less would mean exposing to individual nodes which subset of the database a read or write was from, opening up the possibility of statistical memory leaks. Second, every multiplication requires a network message, so the fundamental bottleneck here is not computation or memory but latency. Because of this, we can already see that secret sharing networks are unfortunately not God protocols; they can do business logic just fine, but they will never be able to do anything more complicated – even crypto verifications, with the exception of a select few crypto verifications specifically tailored to the platform, are in many cases too expensive.

From Currency to EVM

Now, the next problem is, how do we go from this simple toy currency to a generic EVM processor? Well, let us examine the code for the virtual machine inside a single transaction environment. A simplified version of the function looks roughly as follows:

def run_evm(block, tx, msg, code):     pc = 0     gas = msg.gas     stack = []     stack_size = 0     exit = 0     while 1:         op = code[pc]         gas -= 1         if gas < 0 or stack_size < get_stack_req(op):             exit = 1         if op == ADD:             x = stack[stack_size]             y = stack[stack_size - 1]             stack[stack_size - 1] = x + y             stack_size -= 1         if op == SUB:             x = stack[stack_size]             y = stack[stack_size - 1]             stack[stack_size - 1] = x - y             stack_size -= 1         ...         if op == JUMP:             pc = stack[stack_size]             stack_size -= 1         ...

The variables involved are:

The code
The stack
The memory
The account state
The program counter

Hence, we can simply store these as records, and for every computational step run a function similar to the following:

op = code[pc] * alive + 256 * (1 - alive) gas -= 1  stack_p1[0] = 0 stack_p0[0] = 0 stack_n1[0] = stack[stack_size] + stack[stack_size - 1] stack_sz[0] = stack_size - 1 new_pc[0] = pc + 1  stack_p1[1] = 0 stack_p0[1] = 0 stack_n1[1] = stack[stack_size] * stack[stack_size - 1] stack_sz[1] = stack_size - 1 new_pc[1] = pc + 1 ... stack_p1[86] = 0 stack_p0[86] = 0 stack_n1[86] = stack[stack_size - 1] stack_sz[86] = stack_size - 1 new_pc[86] = stack[stack_size] ... stack_p1[256] = 0 stack_p0[256] = 0 stack_n1[256] = 0 stack_sz[256] = 0 new_pc[256] = 0  pc = new_pc[op] stack[stack_size + 1] = stack_p1[op] stack[stack_size] = stack_p0[op] stack[stack_size - 1] = stack_n1[op] stack_size = stack_sz[op] pc = new_pc[op] alive *= (gas  0) * (stack_size  0)

Essentially, we compute the result of every single opcode in parallel, and then pick the correct one to update the state. The alive variable starts off at 1, and if the alive variable at any point switches to zero, then all operations from that point simply do nothing. This seems horrendously inefficient, and it is, but remember: the bottleneck is not computation time but latency. Everything above can be parallelized. In fact, the astute reader may even notice that the entire process of running every opcode in parallel has only O(n) complexity in the number of opcodes (particularly if you pre-grab the top few items of the stack into specified variables for input as well as output, which we did not do for brevity), so it is not even the most computationally intensive part (if there are more accounts or storage slots than opcodes, which seems likely, the database updates are). At the end of every N steps (or for even less information leakage every power of two of steps) we reconstitute the alive variable and if we see that alive = 0 then we halt.

In an EVM with many participants, the database will likely be the largest overhead. To mitigate this problem, there are likely clever information leakage tradeoffs that can be made. For example, we already know that most of the time code is read from sequential database indices. Hence, one approach might be to store the code as a sequence of large numbers, each large number encoding many opcodes, and then use bit decomposition protocols to read off individual opcodes from a number once we load it. There are also likely many ways to make the virtual machine fundamentally much more efficient; the above is meant, once again, as a proof of concept to show how a secret sharing DAO is fundamentally possible, not anything close to an optimal implementation. Additionally, we can look into architectures similar to the ones used in scalability 2.0 techniques to highly compartmentalize the state to further increase efficiency.

Updating the N

The SMPC mechanism described above assumes an existing N parties involved, and aims to be secure against any minority of them (or in some designs at least any minority less than 1/4 or 1/3) colluding. However, blockchain protocols need to theoretically last forever, and so stagnant economic sets do not work; rather, we need to select the consensus participants using some mechanism like proof of stake. To do this, an example protocol would work as follows:

The secret sharing DAO's time is divided into "epochs", each perhaps somewhere between an hour and a week long.
During the first epoch, the participants are set to be the top N participants during the genesis sale.
At the end of an epoch, anyone has the ability to sign up to be one of the participants in the next round by putting down a deposit. N participants are randomly chosen, and revealed.
A "decentralized handoff protocol" is carried out, where the N participants simultaneously split their shares among the new N, and each of the new N reconstitutes their share from the pieces that they received - essentially, the exact same protocol as was used for multiplication. Note that this protocol can also be used to increase or decrease the number of participants.

All of the above handles decentralization assuming honest participants; but in a cryptocurrency protocol we also need incentives. To accomplish that, we use a set of primitives called verifiable secret sharing, that allow us to determine whether a given node was acting honestly throughout the secret sharing process. Essentially, this process works by doing the secret sharing math in parallel on two different levels: using integers, and using elliptic curve points (other constructions also exist, but because cryptocurrency users are most familiar with the secp256k1 elliptic curve we'll use that). Elliptic curve points are convenient because they have a commutative and associative addition operator - in essence, they are magic objects which can be added and subtracted much like numbers can. You can convert a number into a point, but not a point into a number, and we have the property that number_to_point(A + B) = number_to_point(A) + number_to_point(B). By doing the secret sharing math on the number level and the elliptic curve point level at the same time, and publicizing the elliptic curve points, it becomes possible to verify malfeasance. For efficiency, we can probably use a Schellingcoin-style protocol to allow nodes to punish other nodes that are malfeasant.

Applications

So, what do we have? If the blockchain is a decentralized computer, a secret sharing DAO is a decentralized computer with privacy. The secret sharing DAO pays dearly for this extra property: a network message is required per multiplication and per database access. As a result, gas costs are likely to be much higher than Ethereum proper, limiting the computation to only relatively simple business logic, and barring the use of most kinds of cryptographic calculations. Scalability technology may be used to partially offset this weakness, but ultimately there is a limit to how far you can get. Hence, this technology will probably not be used for every use case; instead, it will operate more like a special-purpose kernel that will only be employed for specific kinds of decentralized applications. Some examples include:

Medical records - keeping the data on a private decentralized platform can potentially open the door for an easy-to-use and secure health information system that keeps patients in control of their data. Particularly, note that proprietary diagnosis algorithms could run inside the secret sharing DAO, allowing medical diagnosis as a service based on data from separate medical checkup firms without running the risk that they will intentionally or unintentionally expose your private details to insurers, advertisers or other firms.
Private key escrow - a decentralized M-of-N alternative to centralized password recovery; could be used for financial or non-financial applications
Multisig for anything - even systems that do not natively support arbitrary access policies, or even M-of-N multisignature access, now will, since as long as they support cryptography you can stick the private key inside of a secret sharing DAO.
Reputation systems - what if reputation scores were stored inside a secret sharing DAO so you could privately assign reputation to other users, and have your assignment count towards the total reputation of that user, without anyone being able to see your individual assignments?
Private financial systems - secret sharing DAOs could provide an alternative route to Zerocash-style fully anonymous currency, except that here the functionality could be much more easily extended to decentralized exchange and more complex smart contracts. Business users may want to leverage some of the benefits of running their company on top of crypto without necessarily exposing every single one of their internal business processes to the general public.
Matchmaking algorithms - find employers, employees, dating partners, drivers for your next ride on Decentralized Uber, etc, but doing the matchmaking algorithm computations inside of SMPC so that no one sees any information about you unless the algorithm determines that you are a perfect match.

Essentially, one can think of SMPC as offering a set of tools roughly similar to that which it has been theorized would be offered by cryptographically secure code obfuscation, except with one key difference: it actually works on human-practical time scales.

Further Consequences

Aside from the applications above, what else will secret sharing DAOs bring? Particularly, is there anything to worry about? As it turns out, just like with blockchains themselves, there are a few concerns. The first, and most obvious, issue is that secret sharing DAOs will substantially increase the scope of applications that can be carried out in a completely private fashion. Many advocates of blockchain technology often base a large part of their argument on the key point that while blockchain-based currencies offer an unprecedented amount of anonymity in the sense of not linking addresses to individual identities, they are at the same time the most public form of currency in the world because every transaction is located on a shared ledger. Here, however, the first part remains, but the second part disappears completely. What we have left is essentially total anonymity.

If it turns out to be the case that this level of anonymity allows for a much higher degree of criminal activity, and the public is not happy with the tradeoff that the technology brings, then we can predict that governments and other institutions in general, perhaps even alongside volunteer vigilante hackers, will try their best to take these systems down, and perhaps they would even be justified. Fortunately for these attackers, however, secret sharing DAOs do have an inevitable backdoor: the 51% attack. If 51% of the maintainers of a secret sharing DAO at some particular time decide to collude, then they can uncover any of the data that is under their supervision. Furthermore, this power has no statute of limitations: if a set of entities who formed over half of the maintaining set of a secret sharing DAO at some point many years ago collude, then even then the group would be able to unearth the information from that point in time. In short, if society is overwhelmingly opposed to something being done inside of a secret sharing DAO, there will be plenty of opportunity for the operators to collude to stop or reveal what's going on.

A second, and subtler, issue is that the concept of secret sharing DAOs drives a stake through a cherished fact of cryptoeconomics: that private keys are not securely tradeable. Many protocols explicitly, or implicitly, rely on this idea, including non-outsourceable proof of work puzzles, Vlad Zamfir and Pavel Kravchenko's proof of custody, economic protocols that use private keys as identities, any kind of economic status that aims to be untradeable, etc. Online voting systems often have the requirement that it should be impossible to prove that you voted with a particular key, so as to prevent vote selling; with secret sharing DAOs, the problem is that now you actually can sell your vote, rather simply: by putting your private key into a contract inside of a secret sharing DAO, and renting out access.

The consequences of this ability to sell private keys are quite far reaching - in fact, they go so far as to almost threaten the security of the strongest available system underlying blockchain security: proof of stake. The potential concern is this: proof of stake derives its security from the fact that users have security deposits on the blockchain, and these deposits can potentially be taken away if the user misacts in some fashion (double-voting, voting for a fork, not voting at all, etc). Here, private keys become tradeable, and so security deposits become tradeable as well. We must ask the question: does this compromise proof of stake?

Fortunately, the answer is no. First of all, there are strong lemon-theoretic arguments for why no one would actually want to sell their deposit. If you have a deposit of $ 10, to you that's worth $ 10 minus the tiny probability that you will get hacked. But if you try to sell that deposit to someone else, they will have a deposit which is worth $ 10, unless you decide to use your private key to double-vote and thus destroy the deposit. Hence, from their point of view, there is a constant overhanging risk that you will act to take their deposit away, and you personally have no incentive not to do that. The very fact that you are trying to sell off your deposit should make them suspicious. Hence, from their point of view, your deposit might only be worth, say, $ 8. You have no reason to sacrifice $ 10 for $ 8, so as a rational actor you will keep the deposit to yourself.

Second, if the private key was in the secret sharing DAO right from the start, then by transferring access to the key you would personally lose access to it, so you would actually transfer the authority and the liability at the same time - from an economic standpoint, the effect on the system would be exactly the same as if one of the deposit holders simply had a change of personality at some point during the process. In fact, secret sharing DAOs may even improve proof of stake, by providing a more secure platform for users to participate in decentralized stake pools even in protocols like Tendermint, which do not natively support such functionality.

There are also other reasons why the theoretical attacks that secret sharing DAOs make possible may in fact fail in practice. To take one example, consider the case of non-outsourceable puzzles, computational problems which try to prove ownership of a private key and a piece of data at the same time. One kind of implementation of a non-outsourceable puzzle, used by Permacoin, involves a computation which needs to "bounce" back and forth between the key and the data hundreds of thousands of times. This is easy to do if you have the two pieces of data on the same piece of hardware, but becomes prohibitively slow if the two are separated by a network connection - and over a secret sharing DAO it would be nearly impossible due to the inefficiencies. As a result, one possible conclusion of all this is that secret sharing DAOs will lead to the standardization of a signature scheme which requires several hundred millions of rounds of computation - preferably with lots and lots of serial multiplication - to compute, at which point every computer, phone or internet-of-things microchip would have a built-in ASIC to do it trivially, secret sharing DAOs would be left in the dust, and we would all move on with our lives.

How Far Away?

So what is left before secret sharing DAO technology can go mainstream? In short, quite a bit, but not too much. At first, there is certainly a moderate amount of technical engineering involved, at least on the protocol level. Someone needs to formalize an SMPC implementation, together with how it would be combined with an EVM implementation, probably with many restrictions for efficiency (eg. hash functions inside of SMPC are very expensive, so Merkle tree storage may disappear in favor of every contract having a finite number of storage slots), a punishment, incentive and consensus framework and a hypercube-style scalability framework, and then release the protocol specification. From that point, it's a few months of development in Python (Python should be fine, as by far the primary bottleneck will be network latency, not computation), and we'll have a working proof of concept.

Secret sharing and SMPC technology has been out there for many years, and academic cryptographers have been talking about how to build privacy-preserving applications using M-of-N-based primitives and related technologies such as private information retrieval for over a decade. The key contribution made by Bitcoin, however, is the idea that M-of-N frameworks in general can be much more easily bootstrapped if we add in an economic layer. A secret sharing DAO with a currency built in would provide incentives for individuals to participate in maintaining the network, and would bootstrap it until the point where it could be fully self-sustaining on internal applications. Thus, altogether, this technology is quite possible, and not nearly so far away; it is only a matter of time until someone does it.

The post Secret Sharing DAOs: The Other Crypto 2.0 appeared first on ethereum blog.

ethereum blog

26. Dezember 2014/0 Kommentare/von christian

CryptoAssets

Slasher Ghost, and Other Developments in Proof of Stake

Special thanks to Vlad Zamfir and Zack Hess for ongoing research and discussions on proof-of-stake algorithms and their own input into Slasher-like proposals

One of the hardest problems in cryptocurrency development is that of devising effective consensus algorithms. Certainly, relatively passable default options exist. At the very least it is possible to rely on a Bitcoin-like proof of work algorithm based on either a randomly-generated circuit approach targeted for specialized-hardware resitance, or failing that simple SHA3, and our existing GHOST optimizations allow for such an algorithm to provide block times of 12 seconds. However, proof of work as a general category has many flaws that call into question its sustainability as an exclusive source of consensus; 51% attacks from altcoin miners, eventual ASIC dominance and high energy inefficiency are perhaps the most prominent. Over the last few months we have become more and more convinced that some inclusion of proof of stake is a necessary component for long-term sustainability; however, actually implementing a proof of stake algorithm that is effective is proving to be surprisingly complex.

The fact that Ethereum includes a Turing-complete contracting system complicates things further, as it makes certain kinds of collusion much easier without requiring trust, and creates a large pool of stake in the hands of decentralized entities that have the incentive to vote with the stake to collect rewards, but which are too stupid to tell good blockchains from bad. What the rest of this article will show is a set of strategies that deal with most of the issues surrounding proof of stake algorithms as they exist today, and a sketch of how to extend our current preferred proof-of-stake algorithm, Slasher, into something much more robust.

Historical Overview: Proof of stake and Slasher

If you’re not yet well-versed in the nuances of proof of stake algorithms, first read: https://blog.ethereum.org/2014/07/05/stake/

The fundamental problem that consensus protocols try to solve is that of creating a mechanism for growing a blockchain over time in a decentralized way that cannot easily be subverted by attackers. If a blockchain does not use a consensus protocol to regulate block creation, and simply allows anyone to add a block at any time, then an attacker or botnet with very many IP addresses could flood the network with blocks, and particularly they can use their power to perform double-spend attacks – sending a payment for a product, waiting for the payment to be confirmed in the blockchain, and then starting their own “fork” of the blockchain, substituting the payment that they made earlier with a payment to a different account controlled by themselves, and growing it longer than the original so everyone accepts this new blockchain without the payment as truth.

The general solution to this problem involves making a block “hard” to create in some fashion. In the case of proof of work, each block requires computational effort to produce, and in the case of proof of stake it requires ownership of coins – in most cases, it’s a probabilistic process where block-making privileges are doled out randomly in proportion to coin holdings, and in more exotic “negative block reward” schemes anyone can create a block by spending a certain quantity of funds, and they are compensated via transaction fees. In any of these approaches, each chain has a “score” that roughly reflects the total difficulty of producing the chain, and the highest-scoring chain is taken to represent the “truth” at that particular time.

For a detailed overview of some of the finer points of proof of stake, see the above-linked article; for those readers who are already aware of the issues I will start off by presenting a semi-formal specification for Slasher:

Blocks are produced by miners; in order for a block to be valid it must satisfy a proof-of-work condition. However, this condition is relatively weak (eg. we can target the mining reward to something like 0.02x the genesis supply every year)
Every block has a set of designated signers, which are chosen beforehand (see below). For a block with valid PoW to be accepted as part of the chain it must be accompanied by signatures from at least two thirds of its designated signers.
When block N is produced, we say that the set of potential signers of block N + 3000 is the set of addresses such that sha3(address + block[N].hash) < block[N].balance(address) * D2 where D2 is a difficulty parameter targeting 15 signers per block (ie. if block N has less than 15 signers it goes down otherwise it goes up). Note that the set of potential signers is very computationally intensive to fully enumerate, and we don’t try to do so; instead we rely on signers to self-declare.
If a potential signer for block N + 3000 wants to become a designated signer for that block, they must send a special transaction accepting this responsibility and that transaction must get included between blocks N + 1 and N + 64. The set of designated signers for block N + 3000 is the set of all individuals that do this. This “signer must confirm” mechanism helps ensure that the majority of signers will actually be online when the time comes to sign. For blocks 0 … 2999, the set of signers is empty, so proof of work alone suffices to create those blocks.
When a designated signer adds their signature to block N + 3000, they are scheduled to receive a reward in block N + 6000.
If a signer signs two different blocks at height N + 3000, then if someone detects the double-signing before block N + 6000 they can submit an “evidence” transaction containing the two signatures, destroying the signer’s reward and transferring a third of it to the whistleblower.
If there is an insufficient number of signers to sign at a particular block height h, a miner can produce a block with height h+1 directly on top of the block with height h-1 by mining at an 8x higher difficulty (to incentivize this, but still make it less attractive than trying to create a normal block, there is a 6x higher reward). Skipping over two blocks has higher factors of 16x diff and 12x reward, three blocks 32x and 24x, etc.

Essentially, by explicitly punishing double-signing, Slasher in a lot of ways, although not all, makes proof of stake act like a sort of simulated proof of work. An important incidental benefit of Slasher is the non-revert property. In proof of work, sometimes after one node mines one block some other node will immediately mine two blocks, and so some nodes will need to revert back one block upon seeing the longer chain. Here, every block requires two thirds of the signers to ratify it, and a signer cannot ratify two blocks at the same height without losing their gains in both chains, so assuming no malfeasance the blockchain will never revert. From the point of view of a decentralized application developer, this is a very desirable property as it means that “time” only moves in one direction, just like in a server-based environment.

However, Slasher is still vulnerable to one particular class of attack: long-range attacks. Instead of trying to start a fork from ten blocks behind the current head, suppose that an attacker tries to start a fork starting from ten thousand blocks behind, or even the genesis block – all that matters is that the depth of the fork must be greater than the duration of the reward lockup. At that point, because users’ funds are unlocked and they can move them to a new address to escape punishment, users have no disincentive against signing on both chains. In fact, we may even expect to see a black market of people selling their old private keys, culminating with an attacker single-handedly acquiring access to the keys that controlled over 50% of the currency supply at some point in history.

One approach to solving the long-range double-signing problem is transactions-as-proof-of-stake, an alternative PoS solution that does not have an incentive to double-sign because it’s the transactions that vote, and there is no reward for sending a transaction (in fact there’s a cost, and the reward is outside the network); however, this does nothing to stop the black key market problem. To properly deal with that issue, we will need to relax a hidden assumption.

Subjective Scoring and Trust

For all its faults, proof of work does have some elegant economic properties. Particularly, because proof of work requires an externally rivalrous resource, something with exists and is consumed outside the blockchain, in order to generate blocks (namely, computational effort), launching a fork against a proof of work chain invariably requires having access to, and spending, a large quantity of economic resources. In the case of proof of stake, on the other hand, the only scarce value involved is value within the chain, and between multiple chains that value is not scarce at all. No matter what algorithm is used, in proof of stake 51% of the owners of the genesis block could eventually come together, collude, and produce a longer (ie. higher-scoring) chain than everyone else.

This may seem like a fatal flaw, but in reality it is only a flaw if we implicitly accept an assumption that is made in the case of proof of work: that nodes have no knowledge of history. In a proof-of-work protocol, a new node, having no direct knowledge of past events and seeing nothing but the protocol source code and the set of messages that have already been published, can join the network at any point and determine the score of all possible chains, and from there the block that is at the top of the highest-scoring main chain. With proof of stake, as we described, such a property cannot be achieved, since it’s very cheap to acquire historical keys and simulate alternate histories. Thus, we will relax our assumptions somewhat: we will say that we are only concerned with maintaining consensus between a static set of nodes that are online at least once every N days, allowing these nodes to use their own knowledge of history to reject obvious long-range forks using some formula, and new nodes or long-dormant nodes will need to specify a “checkpoint” (a hash of a block representing what the rest of the network agrees is a recent state) in order to get back onto the consensus.

Such an approach is essentially a hybrid between the pure and perhaps harsh trust-no-one logic of Bitcoin and the total dependency on socially-driven consensus found in networks like Ripple. In Ripple’s case, users joining the system need to select a set of nodes that they trust (or, more precisely, trust not to collude) and rely on those nodes during every step of the consensus process. In the case of Bitcoin, the theory is that no such trust is required and the protocol is completely self-contained; the system works just as well between a thousand isolated cavemen with laptops on a thousand islands as it does in a strongly connected society (in fact, it might work better with island cavemen, since without trust collusion is more difficult). In our hybrid scheme, users need only look to the society outside of the protocol exactly once – when they first download a client and find a checkpoint – and can enjoy Bitcoin-like trust properties starting from that point.

In order to determine which trust assumption is the better one to take, we ultimately need to ask a somewhat philosophical question: do we want our consensus protocols to exist as absolute cryptoeconomic constructs completely independent of the outside world, or are we okay with relying heavily on the fact that these systems exist in the context of a wider society? Although it is indeed a central tenet of mainstream cryptocurrency philosophy that too much external dependence is dangerous, arguably the level of independence that Bitcoin affords us in reality is no greater than that provided by the hybrid model. The argument is simple: even in the case of Bitcoin, a user must also take a leap of trust upon joining the network – first by trusting that they are joining a protocol that contains assets that other people find valuable (eg. how does a user know that bitcoins are worth $ 380 each and dogecoins only $ 0.0004? Especially with the different capabilities of ASICs for different algorithms, hashpower is only a very rough estimate), and second by trusting that they are downloading the correct software package. In both the supposedly “pure” model and the hybrid model there is always a need to look outside the protocol exactly once. Thus, on the whole, the gain from accepting the extra trust requirement (namely, environmental friendliness and security against oligopolistic mining pools and ASIC farms) is arguably worth the cost.

Additionally, we may note that, unlike Ripple consensus, the hybrid model is still compatible with the idea of blockchains “talking” to each each other by containing a minimal “light” implementation of each other’s protocols. The reason is that, while the scoring mechanism is not “absolute” from the point of view of a node without history suddenly looking at every block, it is perfectly sufficient from the point of view of an entity that remains online over a long period of time, and a blockchain certainly is such an entity.

So far, there have been two major approaches that followed some kind of checkpoint-based trust model:

Developer-issued checkpoints – the client developer issues a new checkpoint with each client upgrade (eg. used in PPCoin)
Revert limit – nodes refuse to accept forks that revert more than N (eg. 3000) blocks (eg. used in Tendermint)

The first approach has been roundly criticized by the cryptocurrency community for being too centralized. The second, however, also has a flaw: a powerful attacker can not only revert a few thousand blocks, but also potentially split the network permanently. In the N-block revert case, the strategy is as follows. Suppose that the network is currently at block 10000, and N = 3000. The attacker starts a secret fork, and grows it by 3001 blocks faster than the main network. When the main network gets to 12999, and some node produces block 13000, the attacker reveals his own fork. Some nodes will see the main network’s block 13000, and refuse to switch to the attacker’s fork, but the nodes that did not yet see that block will be happy to revert from 12999 to 10000 and then accept the attacker’s fork. From there, the network is permanently split.

Fortunately, one can actually construct a third approach that neatly solves this problem, which we will call exponentially subjective scoring. Essentially, instead of rejecting forks that go back too far, we simply penalize them on a graduating scale. For every block, a node maintains a score and a “gravity” factor, which acts as a multiplier to the contribution that the block makes to the blockchain’s score. The gravity of the genesis block is 1, and normally the gravity of any other block is set to be equal to the gravity of its parent. However, if a node receives a block whose parent already has a chain of N descendants (ie. it’s a fork reverting N blocks), that block’s gravity is penalized by a factor of 0.99^N, and the penalty propagates forever down the chain and stacks multiplicatively with other penalties.

That is, a fork which starts 1 block ago will need to grow 1% faster than the main chain in order to overtake it, a fork which starts 100 blocks ago will need to grow 2.718 times as quickly, and a fork which starts 3000 blocks ago will need to grow 12428428189813 times as quickly – clearly an impossibility with even trivial proof of work.

The algorithm serves to smooth out the role of checkpointing, assigning a small “weak checkpoint” role to each individual block. If an attacker produces a fork that some nodes hear about even three blocks earlier than others, those two chains will need to stay within 3% of each other forever in order for a network split to maintain itself.

There are other solutions that could be used aside from, or even alongside ESS; a particular set of strategies involves stakeholders voting on a checkpoint every few thousand blocks, requiring every checkpoint produced to reflect a large consensus of the majority of the current stake (the reason the majority of the stake can’t vote on every block is, of course, that having that many signatures would bloat the blockchain).

Slasher Ghost

The other large complexity in implementing proof of stake for Ethereum specifically is the fact that the network includes a Turing-complete financial system where accounts can have arbitrary permissions and even permissions that change over time. In a simple currency, proof of stake is relatively easy to accomplish because each unit of currency has an unambiguous owner outside the system, and that owner can be counted on to participate in the stake-voting process by signing a message with the private key that owns the coins. In Ethereum, however, things are not quite so simple: if we do our job promoting proper wallet security right, the majority of ether is going to be stored in specialized storage contracts, and with Turing-complete code there is no clear way of ascertaining or assigning an “owner”.

One strategy that we looked at was delegation: requiring every address or contract to assign an address as a delegate to sign for them, and that delegate account would have to be controlled by a private key. However, there is a problem with any such approach. Suppose that a majority of the ether in the system is actually stored in application contracts (as opposed to personal storage contracts); this includes deposits in SchellingCoins and other stake-based protocols, security deposits in probabilistic enforcement systems, collateral for financial derivatives, funds owned by DAOs, etc. Those contracts do not have an owner even in spirit; in that case, the fear is that the contract will default to a strategy of renting out stake-voting delegations to the highest bidder. Because attackers are the only entities willing to bid more than the expected return from the delegation, this will make it very cheap for an attacker to acquire the signing rights to large quantities of stake.

The only solution to this within the delegation paradigm is to make it extremely risky to dole out signing privileges to untrusted parties; the simplest approach is to modify Slasher to require a large deposit, and slash the deposit as well as the reward in the event of double-signing. However, if we do this then we are essentially back to entrusting the fate of a large quantity of funds to a single private key, thereby defeating much of the point of Ethereum in the first place.

Fortunately, there is one alternative to delegation that is somewhat more effective: letting contracts themselves sign. To see how this works, consider the following protocol:

There is now a SIGN opcode added.
A signature is a series of virtual transactions which, when sequentially applied to the state at the end of the parent block, results in the SIGN opcode being called. The nonce of the first VTX in the signature must be the prevhash being signed, the nonce of the second must be the prevhash plus one, and so forth (alternatively, we can make the nonces -1, -2, -3 etc. and require the prevhash to be passed in through transaction data so as to be eventually supplied as an input to the SIGN opcode).
When the block is processed, the state transitions from the VTXs are reverted (this is what is meant by “virtual”) but a deposit is subtracted from each signing contract and the contract is registered to receive the deposit and reward in 3000 blocks.

Basically, it is the contract’s job to determine the access policy for signing, and the contract does this by placing the SIGN opcode behind the appropriate set of conditional clauses. A signature now becomes a set of transactions which together satisfy this access policy. The incentive for contract developers to keep this policy secure, and not dole it out to anyone who asks, is that if it is not secure then someone can double-sign with it and destroy the signing deposit, taking a portion for themselves as per the Slasher protocol. Some contracts will still delegate, but this is unavoidable; even in proof-of-stake systems for plain currencies such as NXT, many users end up delegating (eg. DPOS even goes so far as to institutionalize delegation), and at least here contracts have an incentive to delegate to an access policy that is not likely to come under the influence of a hostile entity – in fact, we may even see an equilibrium where contracts compete to deliver secure blockchain-based stake pools that are least likely to double-vote, thereby increasing security over time.

However, the virtual-transactions-as-signatures paradigm does impose one complication: it is no longer trivial to provide an evidence transaction showing two signatures by the same signer at the same block height. Because the result of a transaction execution depends on the starting state, in order to ascertain whether a given evidence transaction is valid one must prove everything up to the block in which the second signature was given. Thus, one must essentially “include” the fork of a blockchain inside of the main chain. To do this efficiently, a relatively simple proposal is a sort of “Slasher GHOST” protocol, where one can include side-blocks in the main chain as uncles. Specifically, we declare two new transaction types:

[block_number, uncle_hash] – this transaction is valid if (1) the block with the given uncle_hash has already been validated, (2) the block with the given uncle_hash has the given block number, and (3) the parent of that uncle is either in the main chain or was included earlier as an uncle. During the act of processing this transaction, if addresses that double-signed at that height are detected, they are appropriately penalized.
[block_number, uncle_parent_hash, vtx] – this transaction is valid if (1) the block with the given uncle_parent_hash has already been validated, (2) the given virtual transaction is valid at the given block height with the state at the end of uncle_parent_hash, and (3) the virtual transaction shows a signature by an address which also signed a block at the given block_number in the main chain. This transaction penalizes that one address.

Essentially, one can think of the mechanism as working like a “zipper”, with one block from the fork chain at a time being zipped into the main chain. Note that for a fork to start, there must exist double-signers at every block; there is no situation where there is a double-signer 1500 blocks into a fork so a whistleblower must “zip” 1499 innocent blocks into a chain before getting to the target block – rather, in such a case, even if 1500 blocks need to be added, each one of them notifies the main chain about five separate malfeasors that double-signed at that height. One somewhat complicated property of the scheme is that the validity of these “Slasher uncles” depends on whether or not the node has validated a particular block outside of the main chain; to facilitate this, we specify that a response to a “getblock” message in the wire protocol must include the uncle-dependencies for a block before the actual block. Note that this may sometimes lead to a recursive expansion; however, the denial-of-service potential is limited since each individual block still requires a substantial quantity of proof-of-work to produce.

Blockmakers and Overrides

Finally, there is a third complication. In the hybrid-proof-of-stake version of Slasher, if a miner has an overwhelming share of the hashpower, then the miner can produce multiple versions of each block, and send different versions to different parts of the network. Half the signers will see and sign one block, half will see and sign another block, and the network will be stuck with two blocks with insufficient signatures, and no signer willing to slash themselves to complete the process; thus, a proof-of-work override will be required, a dangerous situation since the miner controls most of the proof-of-work. There are two possible solutions here:

Signers should wait a few seconds after receiving a block before signing, and only sign stochastically in some fashion that ensures that a random one of the blocks will dominate.
There should be a single “blockmaker” among the signers whose signature is required for a block to be valid. Effectively, this transfers the “leadership” role from a miner to a stakeholder, eliminating the problem, but at the cost of adding a dependency on a single party that now has the ability to substantially inconvenience everyone by not signing, or unintentionally by being the target of a denial-of-service attack. Such behavior can be disincentivized by having the signer lose part of their deposit if they do not sign, but even still this will result in a rather jumpy block time if the only way to get around an absent blockmaker is using a proof-of-work override.

One possible solution to the problem in (2) is to remove proof of work entirely (or almost entirely, keeping a minimal amount for anti-DDoS value), replacing it with a mechanism that Vlad Zamfir has coined “delegated timestamping”. Essentially, every block must appear on schedule (eg. at 15 second intervals), and when a block appears the signers vote 1 if the block was on time, or 0 if the block was too early or too late. If the majority of the signers votes 0, then the block is treated as invalid – kept in the chain in order to give the signers their fair reward, but the blockmaker gets no reward and the state transition gets skipped over. Voting is incentivized via schellingcoin – the signers whose vote agrees with the majority get an extra reward, so assuming that everyone else is going to be honest everyone has the incentive to be honest, in a self-reinforcing equilibrium. The theory is that a 15-second block time is too fast for signers to coordinate on a false vote (the astute reader may note that the signers were decided 3000 blocks in advance so this is not really true; to fix this we can create two groups of signers, one pre-chosen group for validation and another group chosen at block creation time for timestamp voting).

Putting it all Together

Taken together, we can thus see something like the following working as a functional version of Slasher:

Every block has a designated blockmaker, a set of designated signers, and a set of designated timestampers. For a block to be accepted as part of the chain it must be accompanied by virtual-transactions-as-signatures from the blockmaker, two thirds of the signers and 10 timestampers, and the block must have some minimal proof of work for anti-DDoS reasons (say, targeted to 0.01x per year)
During block N, we say that the set of potential signers of block N + 3000 is the set of addresses such that sha3(address + block[N].hash) < block[N].balance(address) * D2 where D2 is a difficulty parameter targeting 15 signers per block (ie. if block N has less than 15 signers it goes down otherwise it goes up).
If a potential signer for block N + 3000 wants to become a signer, they must send a special transaction accepting this responsibility and supplying a deposit, and that transaction must get included between blocks N + 1 and N + 64. The set of designated signers for block N + 3000 is the set of all individuals that do this, and the blockmaker is the designated signer with the lowest value for sha3(address + block[N].hash). If the signer set is empty, no block at that height can be made. For blocks 0 … 2999, the blockmaker and only signer is the protocol developer.
The set of timestampers of the block N + 3000 is the set of addresses such that sha3(address + block[N].hash) < block[N].balance(address) * D3, where D3 is targeted such that there is an average of 20 timestampers each block (ie. if block N has less than 20 timestampers it goes down otherwise it goes up).
Let T be the timestamp of the genesis block. When block N + 3000 is released, timestampers can supply virtual-transactions-as-signatures for that block, and have the choice of voting 0 or 1 on the block. Voting 1 means that they saw the block within 7.5 seconds of time T + (N + 3000) * 15, and voting 0 means that they received the block when the time was outside that range. Note that nodes should detect if their clocks are out of sync with everyone else’s clocks on the blockchain, and if so adjust their system clocks.
Timestampers who voted along with the majority receive a reward, other timestampers get nothing.
The designated signers for block N + 3000 have the ability to sign that block by supplying a set of virtual-transactions-as-a-signature. All designated signers who sign are scheduled to receive a reward and their returned deposit in block N + 6000. Signers who skipped out are scheduled to receive their returned deposit minus twice the reward (this means that it’s only economically profitable to sign up as a signer if you actually think there is a chance greater than 2/3 that you will be online).
If the majority timestamper vote is 1, the blockmaker is scheduled to receive a reward and their returned deposit in block N + 6000. If the majority timestamper vote is 0, the blockmaker is scheduled to receive their deposit minus twice the reward, and the block is ignored (ie. the block is in the chain, but it does not contribute to the chain’s score, and the state of the next block starts from the end state of the block before the rejected block).
If a signer signs two different blocks at height N + 3000, then if someone detects the double-signing before block N + 6000 they can submit an “evidence” transaction containing the two signatures to either or both chains, destroying the signer’s reward and deposit and transferring a third of it to the whistleblower.
If there is an insufficient number of signers to sign or the blockmaker is missing at a particular block height h, the designated blockmaker for height h + 1 can produce a block directly on top of the block at height h - 1 after waiting for 30 seconds instead of 15.

After years of research, one thing has become clear: proof of stake is non-trivial – so non-trivial that some even consider it impossible. The issues of nothing-at-stake and long-range attacks, and the lack of mining as a rate-limiting device, require a number of compensatory mechanisms, and even the protocol above does not address the issue of how to randomly select signers. With a substantial proof of work reward, the problem is limited, as block hashes can be a source of randomness and we can mathematically show that the gain from holding back block hashes until a miner finds a hash that favorably selects future signers is usually less than the gain from publishing the block hashes. Without such a reward, however, other sources of randomness such as low-influence functions need to be used.

For Ethereum 1.0, we consider it highly desirable to both not excessively delay the release and not try too many untested features at once; hence, we will likely stick with ASIC-resistant proof of work, perhaps with non-Slasher proof of activity as an addon, and look at moving to a more comprehensive proof of stake model over time.

The post Slasher Ghost, and Other Developments in Proof of Stake appeared first on ethereum blog.

ethereum blog

3. Oktober 2014/0 Kommentare/von christian