Special thanks to Vlad Zamfir for much of the thinking behind multi-chain cryptoeconomic paradigms
First off, a history lesson. In October 2013, when I was visiting Israel as part of my trip around the Bitcoin world, I came to know the core teams behind the colored coins and Mastercoin projects. Once I properly understood Mastercoin and its potential, I was immediately drawn in by the sheer power of the protocol; however, I disliked the fact that the protocol was designed as a disparate ensemble of “features”, providing a subtantial amount of functionality for people to use, but offering no freedom to escape out of that box. Seeking to improve Mastercoin’s potential, I came up with a draft proposal for something called “ultimate scripting” – a general-purpose stack-based programming language that Mastercoin could include to allow two parties to make a contract on an arbitrary mathematical formula. The scheme would generalize savings wallets, contracts for difference, many kinds of gambling, among other features. It was still quite limited, allowing only three stages (open, fill, resolve) and no internal memory and being limited to 2 parties per contract, but it was the first true seed of the Ethereum idea.
I submitted the proposal to the Mastercoin team. They were impressed, but elected not to adopt it too quickly out of a desire to be slow and conservative; a philosophy which the project keeps to to this day and which David Johnston mentioned at the recent Tel Aviv conference as Mastercoin’s primary differentiating feature. Thus, I decided to go out on my own and simply build the thing myself. Over the next three weeks I created the original Ethereum whitepaper (unfortunately now gone, but a still very early version exists here). The basic building blocks were all there, except the progamming language was register-based instead of stack-based, and, because I was/am not skilled enough in p2p networking to build an independent blockchain client from scratch, it was to be built as a meta-protocol on top of Primecoin – not Bitcoin, because I wanted to satisfy the concerns of Bitcoin developers who were angry at meta-protocols bloating the blockchain with extra data.
Once competent developers like Gavin Wood and Jeffrey Wilcke, who did not share my deficiencies in ability to write p2p networking code, joined the project, and once enough people were excited that I saw there would be money to hire more, I made the decision to immediately move to an independent blockchain. The reasoning for this choice I described in my whitepaper in early January:
The advantage of a metacoin protocol is that it can allow for more advanced transaction types, including custom currencies, decentralized exchange, derivatives, etc, that are impossible on top of Bitcoin itself. However, metacoins on top of Bitcoin have one major flaw: simplified payment verification, already difficult with colored coins, is outright impossible on a metacoin. The reason is that while one can use SPV to determine that there is a transaction sending 30 metacoins to address X, that by itself does not mean that address X has 30 metacoins; what if the sender of the transaction did not have 30 metacoins to start with and so the transaction is invalid? Finding out any part of the current state essentially requires scanning through all transactions going back to the metacoin’s original launch to figure out which transactions are valid and which ones are not. This makes it impossible to have a truly secure client without downloading the entire 12 GB Bitcoin blockchain.
Essentially, metacoins don’t work for light clients, making them rather insecure for smartphones, users with old computers, internet-of-things devices, and once the blockchain scales enough for desktop users as well. Ethereum’s independent blockchain, on the other hand, is specifically designed with a highly advanced light client protocol; unlike with meta-protocols, contracts on top of Ethereum inherit the Ethereum blockchain’s light client-friendliness properties fully. Finally, long after that, I realized that by making an independent blockchain allows us to experiment with stronger versions of GHOST-style protocols, safely knocking down the block time to 12 seconds.
So what’s the point of this story? Essentially, had history been different, we easily could have gone the route of being “on top of Bitcoin” right from day one (in fact, we still could make that pivot if desired), but solid technical reasons existed then why we deemed it better to build an independent blockchain, and these reasons still exist, in pretty much exactly the same form, today.
Since a number of readers were expecting a response to how Ethereum as an independent blockchain would be useful even in the face of the recent announcement of a metacoin based on Ethereum technology, this is it. Scalability. If you use a metacoin on BTC, you gain the benefit of having easier back-and-forth interaction with the Bitcoin blockchain, but if you create an independent chain then you have the ability to achieve much stronger guarantees of security particularly for weak devices. There are certainly applications for which a higher degree of connectivity with BTC is important ; for these cases a metacoin would certainly be superior (although note that even an independent blockchain can interact with BTC pretty well using basically the same technology that we’ll describe in the rest of this blog post). Thus, on the whole, it will certainly help the ecosystem if the same standardized EVM is available across all platforms.
Beyond 1.0
However, in the long term, even light clients are an ugly solution. If we truly expect cryptoeconomic platforms to become a base layer for a very large amount of global infrastructure, then there may well end up being so many crypto-transactions altogether that no computer, except maybe a few very large server farms run by the likes of Google and Amazon, is powerful enough to process all of them. Thus, we need to break the fundamental barrier of cryptocurrency: that there need to exist nodes that process every transaction. Breaking that barrier is what gets a cryptoeconomic platform’s database from being merely massively replicated to being truly distributed. However, breaking the barrier is hard, particularly if you still want to maintain the requirement that all of the different parts of the ecosystem should reinforce each other’s security.
To achieve the goal, there are three major strategies:
- Building protocols on top of Ethereum that use Ethereum only as an auditing-backend-of-last-resort, conserving transaction fees.
- Turning the blockchain into something much closer to a high-dimensional interlinking mesh with all parts of the database reinforcing each other over time.
- Going back to a model of one-protocol (or one service)-per-chain, and coming up with mechanisms for the chains to (1) interact, and (2) share consensus strength.
Of these strategies, note that only (1) is ultimately compatible with keeping the blockchain in a form anything close to what the Bitcoin and Ethereum protocols support today. (2) requires a massive redesign of the fundamental infrastructure, and (3) requires the creation of thousands of chains, and for fragility mitigation purposes the optimal approach will be to use thousands of currencies (to reduce the complexity on the user side, we can use stable-coins to essentially create a common cross-chain currency standard, and any slight swings in the stable-coins on the user side would be interpreted in the UI as interest or demurrage so the user only needs to keep track of one unit of account).
We already discussed (1) and (2) in previous blog posts, and so today we will provide an introduction to some of the principles involved in (3).
Multichain
The model here is in many ways similar to the Bitshares model, except that we do not assume that DPOS (or any other POS) will be secure for arbitrarily small chains. Rather, seeing the general strong parallels between cryptoeconomics and institutions in wider society, particularly legal systems, we note that there exists a large body of shareholder law protecting minority stakeholders in real-world companies against the equivalent of a 51% attack (namely, 51% of shareholders voting to pay 100% of funds to themselves), and so we try to replicate the same system here by having every chain, to some degree, “police” every other chain either directly or indirectly through an interlinking transitive graph. The kind of policing required is simple – policing aganist double-spends and censorship attacks from local majority coalitions, and so the relevant guard mechanisms can be implemented entirely in code.
However, before we get to the hard problem of inter-chain security, let us first discuss what actually turns out to be a much easier problem: inter-chain interaction. What do we mean by multiple chains “interacting”? Formally, the phrase can mean one of two things:
- Internal entities (ie. scripts, contracts) in chain A are able to securely learn facts about the state of chain B (information transfer)
- It is possible to create a pair of transactions, T in A and T’ in B, such that either both T and T’ get confirmed or neither do (atomic transactions)
A sufficiently general implementation of (1) implies (2), since “T’ was (or was not) confirmed in B” is a fact about the state of chain B. The simplest way to do this is via Merkle trees, described in more detail here and here; essentially Merkle trees allow the entire state of a blockchain to be hashed into the block header in such a way that one can come up with a “proof” that a particular value is at a particular position in the tree that is only logarithmic in size in the entire state (ie. at most a few kilobytes long). The general idea is that contracts in one chain validate these Merkle tree proofs of contracts in the other chain.
A challenge that is greater for some consensus algorithms than others is, how does the contract in a chain validate the actual blocks in another chain? Essentially, what you end up having is a contract acting as a fully-fledged “light client” for the other chain, processing blocks in that chain and probabilistically verifying transactions (and keeping track of challenges) to ensure security. For this mechanism to be viable, at least some quantity of proof of work must exist on each block, so that it is not possible to cheaply produce many blocks for which it is hard to determine that they are invalid; as a general rule, the work required by the blockmaker to produce a block should exceed the cost to the entire network combined of rejecting it.
Additionally, we should note that contracts are stupid; they are not capable of looking at reputation, social consensus or any other such “fuzzy” metrics of whether or not a given blockchain is valid; hence, purely “subjective” Ripple-style consensus will be difficult to make work in a multi-chain setting. Bitcoin’s proof of work is (fully in theory, mostly in practice) “objective”: there is a precise definition of what the current state is (namely, the state reached by processing the chain with the longest proof of work), and any node in the world, seeing the collection of all available blocks, will come to the same conclusion on which chain (and therefore which state) is correct. Proof-of-stake systems, contrary to what many cryptocurrency developers think, can be secure, but need to be “weakly subjective” – that is, nodes that were online at least once every N days since the chain’s inception will necessarily converge on the same conclusion, but long-dormant nodes and new nodes need a hash as an initial pointer. This is needed to prevent certain classes of unavoidable long-range attacks. Weakly subjective consensus works fine with contracts-as-automated-light-clients, since contracts are always “online”.
Note that it is possible to support atomic transactions without information transfer; TierNolan’s secret revelation protocol can be used to do this even between relatively dumb chains like BTC and DOGE. Hence, in general interaction is not too difficult.
Security
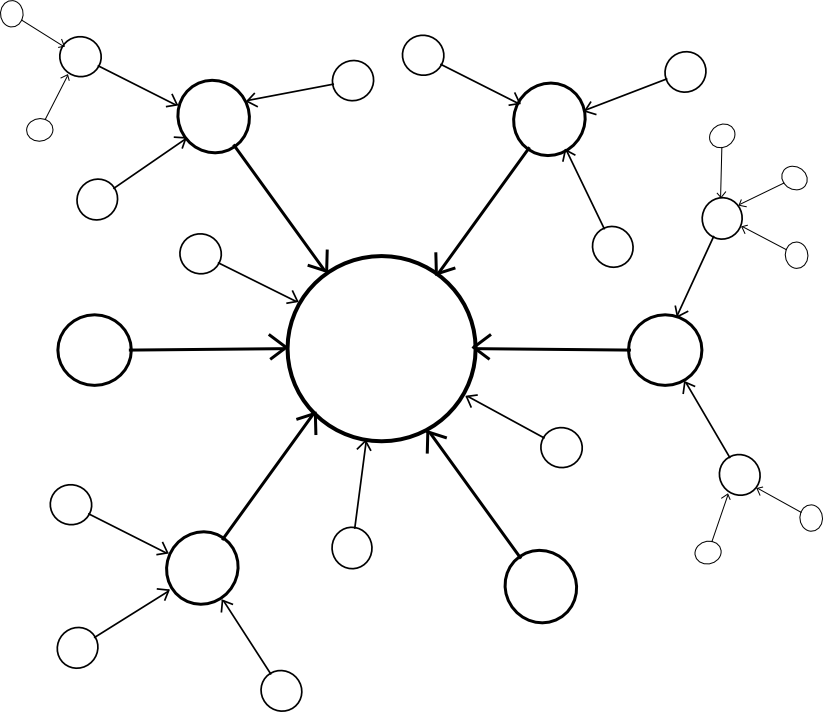
The larger problem, however, is security. Blockchains are vulnerable to 51% attacks, and smaller blockchains are vulnerable to smaller 51% attacks. Ideally, if we want security, we would like for multiple chains to be able to piggyback on each other’s security, so that no chain can be attacked unless every chain is attacked at the same time. Within this framework, there are two major paradigm choices that we can make: centralized or decentralized.
| Centralized | Decentralized |
 |
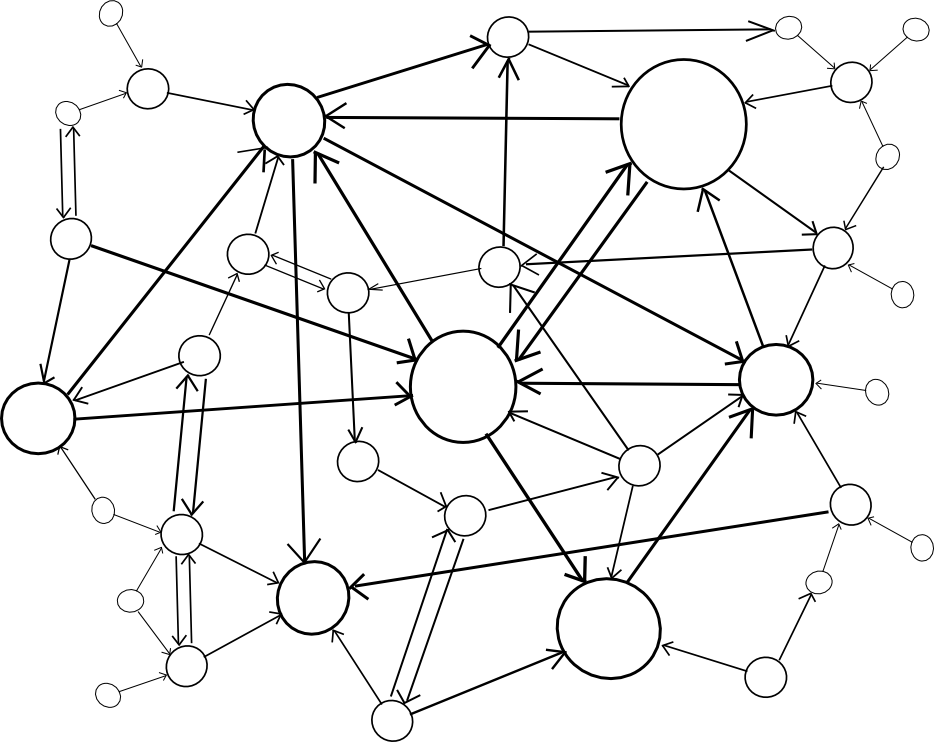 |
A centralized paradigm is essentially every chain, whether directly or indirectly, piggybacking off of a single master chain; Bitcoin proponents often love to see the central chain being Bitcoin, though unfortunately it may be something else since Bitcoin was not exactly designed with the required level of general-purpose functionality in mind. A decentralized paradigm is one that looks vaguely like Ripple’s network of unique node lists, except working across chains: every chain has a list of other consensus mechanisms that it trusts, and those mechanisms together determine block validity.
The centralized paradigm has the benefit that it’s simpler; the decentralized paradigm has the benefit that it allows for a cryptoeconomy to more easily swap out different pieces for each other, so it does not end up resting on decades of outdated protocols. However, the question is, how do we actually “piggyback” on one or more other chains’ security?
To provide an answer to this question, we’ll first come up with a formalism called an assisted scoring function. In general, the way blockchains work is they have some scoring function for blocks, and the top-scoring block becomes the block defining the current state. Assisted scoring functions work by scoring blocks based on not just the blocks themselves, but also checkpoints in some other chain (or multiple chains). The general principle is that we use the checkpoints to determine that a given fork, even though it may appear to be dominant from the point of view of the local chain, can be determined to have come later through the checkpointing process.
A simple approach is that a node penalizes forks where the blocks are too far apart from each other in time, where the time of a block is determined by the median of the earliest known checkpoint of that block in the other chains; this would detect and penalize forks that happen after the fact. However, there are two problems with this approach:
- An attacker can submit the hashes of the blocks into the checkpoint chains on time, and then only reveal the blocks later
- An attacker may simply let two forks of a blockchain grow roughly evenly simultaneously, and then eventually push on his preferred fork with full force
To deal with (2), we can say that only the valid block of a given block number with the earliest average checkpointing time can be part of the main chain, thus essentially completely preventing double-spends or even censorship forks; every new block would have to point to the last known previous block. However, this does nothing against (1). To solve (1), the best general solutions involve some concept of “voting on data availability”; essentially, the participants in the checkpointing contract on each of the other chains would Schelling-vote on whether or not the entire data of the block was available at the time the checkpoint was made, and a checkpoint would be rejected if the vote leans toward “no”.
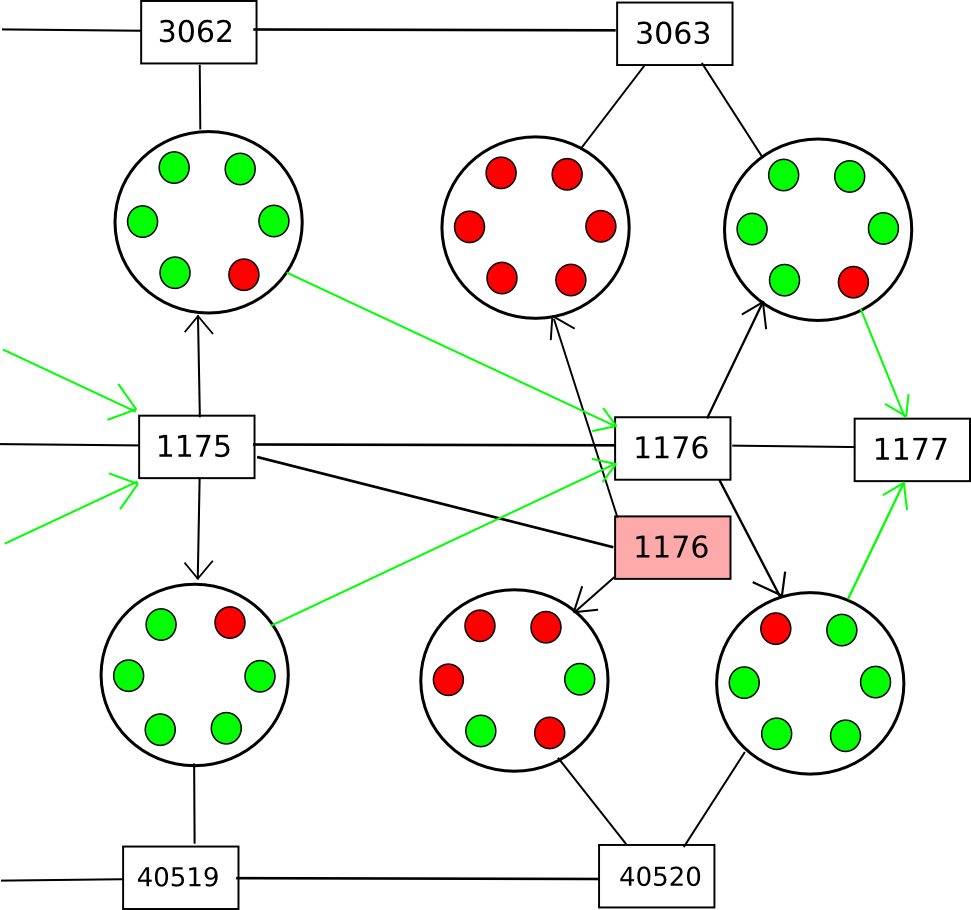
Note that there are two versions of this strategy. The first is a strategy where participants vote on data availability only (ie. that every part of the block is out there online). This allows the voters to be rather stupid, and be able to vote on availability for any blockchain; the process for determining data availability simply consists of repeatedly doing a reverse hash lookup query on the network until all the “leaf nodes” are found and making sure that nothing is missing. A clever way to force nodes to not be lazy when doing this check is to ask them to recompute and vote on the root hash of the block using a different hash function. Once all the data is available, if the block is invalid an efficient Merkle-tree proof of invalidity can be submitted to the contract (or simply published and left for nodes to download when determining whether or not to count the given checkpoint).
The second strategy is less modular: have the Schelling-vote participants vote on block validity. This would make the process somewhat simpler, but at the cost of making it more chain-specific: you would need to have the source code for a given blockchain in order to be able to vote on it. Thus, you would get fewer voters providing security for your chain automatically. Regardless of which of these two strategies is used, the chain could subsidize the Schelling-vote contract on the other chain(s) via a cross-chain exchange.
The Scalability Part
Up until now, we still don’t have any actual “scalability”; a chain is only as secure as the number of nodes that are willing to download (although not process) every block. Of course, there are solutions to this problem: challenge-response protocols and randomly selected juries, both described in the previous blog post on hypercubes, are the two that are currently best-known. However, the solution here is somewhat different: instead of setting in stone and institutionalizing one particular algorithm, we are simply going to let the market decide.
The “market” is defined as follows:
- Chains want to be secure, and want to save on resources. Chains need to select one or more Schelling-vote contracts (or other mechanisms potentially) to serve as sources of security (demand)
- Schelling-vote contracts serve as sources of security (supply). Schelling-vote contracts differ on how much they need to be subsidized in order to secure a given level of participation (price) and how difficult it is for an attacker to bribe or take over the schelling-vote to force it to deliver an incorrect result (quality).
Hence, the cryptoeconomy will naturally gravitate toward schelling-vote contracts that provide better security at a lower price, and the users of those contracts will benefit from being afforded more voting opportunities. However, simply saying that an incentive exists is not enough; a rather large incentive exists to cure aging and we’re still pretty far from that. We also need to show that scalability is actually possible.
The better of the two algorithms described in the post on hypercubes, jury selection, is simple. For every block, a random 200 nodes are selected to vote on it. The set of 200 is almost as secure as the entire set of voters, since the specific 200 are not picked ahead of time and an attacker would need to control over 40% of the participants in order to have any significant chance of getting 50% of any set of 200. If we are separating voting on data availability from voting on validity, then these 200 can be chosen from the set of all participants in a single abstract Schelling-voting contract on the chain, since it’s possible to vote on the data availability of a block without actually understanding anything about the blockchain’s rules. Thus, instead of every node in the network validating the block, only 200 validate the data, and then only a few nodes need to look for actual errors, since if even one node finds an error it will be able to construct a proof and warn everyone else.
Conclusion
So, what is the end result of all this? Essentially, we have thousands of chains, some with one application, but also with general-purpose chains like Ethereum because some applications benefit from the extremely tight interoperability that being inside a single virtual machine offers. Each chain would outsource the key part of consensus to one or more voting mechanisms on other chains, and these mechanisms would be organized in different ways to make sure they’re as incorruptible as possible. Because security can be taken from all chains, a large portion of the stake in the entire cryptoeconomy would be used to protect every chain.
It may prove necessary to sacrifice security to some extent; if an attacker has 26% of the stake then the attacker can do a 51% takeover of 51% of the subcontracted voting mechanisms or Schelling-pools out there; however, 26% of stake is still a large security margin to have in a hypothetical multi-trillion-dollar cryptoeconomy, and so the tradeoff may be worth it.
The true benefit of this kind of scheme is just how little needs to be standardized. Each chain, upon creation, can choose some number of Schelling-voting pools to trust and subsidize for security, and via a customized contract it can adjust to any interface. Merkle trees will need to be compatible with all of the different voting pools, but the only thing that needs to be standardized there is the hash algorithm. Different chains can use different currencies, using stable-coins to provide a reasonably consistent cross-chain unit of value (and, of course, these stable-coins can themselves interact with other chains that implement various kinds of endogenous and exogenous estimators). Ultimately, the vision of one of thousands of chains, with the different chains “buying services” from each other. Services might include data availability checking, timestamping, general information provision (eg. price feeds, estimators), private data storage (potentially even consensus on private data via secret sharing), and much more. The ultimate distributed crypto-economy.
The post Scalability, Part 3: On Metacoin History and Multichain appeared first on ethereum blog.