Schlagwortarchiv für: Proof

Light Clients and Proof of Stake

Special thanks to Vlad Zamfir and Jae Kwon for many of the ideas described in this post

Aside from the primary debate around weak subjectivity, one of the important secondary arguments raised against proof of stake is the issue that proof of stake algorithms are much harder to make light-client friendly. Whereas proof of work algorithms involve the production of block headers which can be quickly verified, allowing a relatively small chain of headers to act as an implicit proof that the network considers a particular history to be valid, proof of stake is harder to fit into such a model. Because the validity of a block in proof of stake relies on stakeholder signatures, the validity depends on the ownership distribution of the currency in the particular block that was signed, and so it seems, at least at first glance, that in order to gain any assurances at all about the validity of a block, the entire block must be verified.

Given the sheer importance of light client protocols, particularly in light of the recent corporate interest in “internet of things” applications (which must often necessarily run on very weak and low-power hardware), light client friendliness is an important feature for a consensus algorithm to have, and so an effective proof of stake system must address it.

Light clients in Proof of Work

In general, the core motivation behind the “light client” concept is as follows. By themselves, blockchain protocols, with the requirement that every node must process every transaction in order to ensure security, are expensive, and once a protocol gets sufficiently popular the blockchain becomes so big that many users become not even able to bear that cost. The Bitcoin blockchain is currently 27 GB in size, and so very few users are willing to continue to run “full nodes” that process every transaction. On smartphones, and especially on embedded hardware, running a full node is outright impossible.

Hence, there needs to be some way in which a user with far less computing power to still get a secure assurance about various details of the blockchain state – what is the balance/state of a particular account, did a particular transaction process, did a particular event happen, etc. Ideally, it should be possible for a light client to do this in logarithmic time – that is, squaring the number of transactions (eg. going from 1000 tx/day to 1000000 tx/day) should only double a light client’s cost. Fortunately, as it turns out, it is quite possible to design a cryptocurrency protocol that can be securely evaluated by light clients at this level of efficiency.

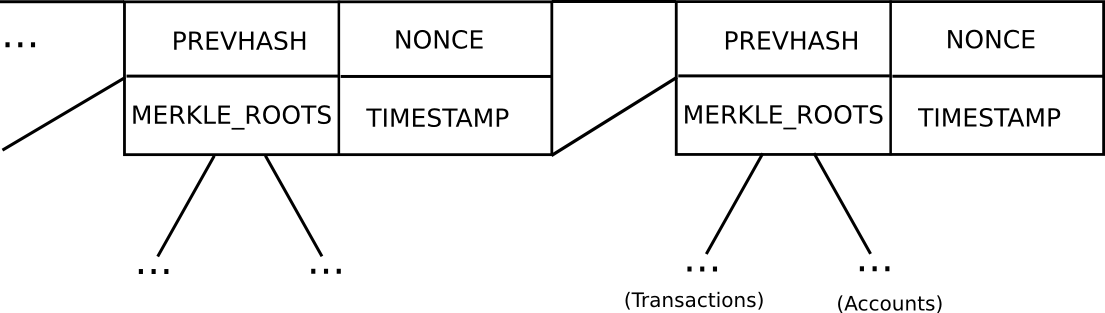
Basic block header model in Ethereum (note that Ethereum has a Merkle tree for transactions and accounts in each block, allowing light clients to easily access more data)

In Bitcoin, light client security works as follows. Instead of constructing a block as a monolithic object containing all of the transactions directly, a Bitcoin block is split up into two parts. First, there is a small piece of data called the block header, containing three key pieces of data:

  • The hash of the previous block header
  • The Merkle root of the transaction tree (see below)
  • The proof of work nonce

Additional data like the timestamp is also included in the block header, but this is not relevant here. Second, there is the transaction tree. Transactions in a Bitcoin block are stored in a data structure called a Merkle tree. The nodes on the bottom level of the tree are the transactions, and then going up from there every node is the hash of the two nodes below it. For example, if the bottom level had sixteen transactions, then the next level would have eight nodes: hash(tx[1] + tx[2]), hash(tx[3] + tx[4]), etc. The level above that would have four nodes (eg. the first node is equal to hash(hash(tx[1] + tx[2]) + hash(tx[3] + tx[4]))), the level above has two nodes, and then the level at the top has one node, the Merkle root of the entire tree.

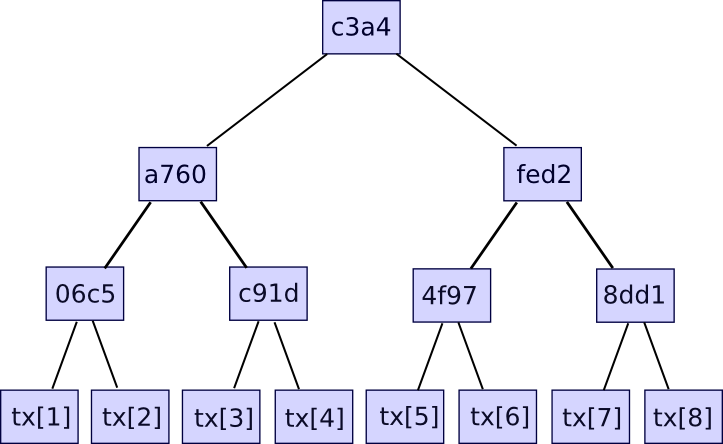
The Merkle root can be thought of as a hash of all the transactions together, and has the same properties that you would expect out of a hash – if you change even one bit in one transaction, the Merkle root will end up completely different, and there is no way to come up with two different sets of transactions that have the same Merkle root. The reason why this more complicated tree construction needs to be used is that it actually allows you to come up with a compact proof that one particular transaction was included in a particular block. How? Essentially, just provide the branch of the tree going down to the transaction:

The verifier will verify only the hashes going down along the branch, and thereby be assured that the given transaction is legitimately a member of the tree that produced a particular Merkle root. If an attacker tries to change any hash anywhere going down the branch, the hashes will no longer match and the proof will be invalid. The size of each proof is equal to the depth of the tree – ie. logarithmic in the number of transactions. If your block contains 220 (ie. ~1 million) transactions, then the Merkle tree will have only 20 levels, and so the verifier will only need to compute 20 hashes in order to verify a proof. If your block contains 230 (ie. ~1 billion) transactions, then the Merkle tree will have 30 levels, and so a light client will be able to verify a transaction with just 30 hashes.

Ethereum extends this basic mechanism with a two additional Merkle trees in each block header, allowing nodes to prove not just that a particular transaction occurred, but also that a particular account has a particular balance and state, that a particular event occurred, and even that a particular account does not exist.

Verifying the Roots

Now, this transaction verification process all assumes one thing: that the Merkle root is trusted. If someone proves to you that a transaction is part of a Merkle tree that has some root, that by itself means nothing; membership in a Merkle tree only proves that a transaction is valid if the Merkle root is itself known to be valid. Hence, the other critical part of a light client protocol is figuring out exactly how to validate the Merkle roots – or, more generally, how to validate the block headers.

First of all, let us determine exactly what we mean by “validating block headers”. Light clients are not capable of fully validating a block by themselves; protocols exist for doing validation collaboratively, but this mechanism is expensive, and so in order to prevent attackers from wasting everyone’s time by throwing around invalid blocks we need a way of first quickly determining whether or not a particular block header is probably valid. By “probably valid” what we mean is this: if an attacker gives us a block that is determined to be probably valid, but is not actually valid, then the attacker needs to pay a high cost for doing so. Even if the attacker succeeds in temporarily fooling a light client or wasting its time, the attacker should still suffer more than the victims of the attack. This is the standard that we will apply to proof of work, and proof of stake, equally.

In proof of work, the process is simple. The core idea behind proof of work is that there exists a mathematical function which a block header must satisfy in order to be valid, and it is computationally very intensive to produce such a valid header. If a light client was offline for some period of time, and then comes back online, then it will look for the longest chain of valid block headers, and assume that that chain is the legitimate blockchain. The cost of spoofing this mechanism, providing a chain of block headers that is probably-valid-but-not-actually-valid, is very high; in fact, it is almost exactly the same as the cost of launching a 51% attack on the network.

In Bitcoin, this proof of work condition is simple: sha256(block_header) < 2**187 (in practice the “target” value changes, but once again we can dispense of this in our simplified analysis). In order to satisfy this condition, miners must repeatedly try different nonce values until they come upon one such that the proof of work condition for the block header is satisfied; on average, this consumes about 269 computational effort per block. The elegant feature of Bitcoin-style proof of work is that every block header can be verified by itself, without relying on any external information at all. This means that the process of validating the block headers can in fact be done in constant time – download 80 bytes and run a hash of it – even better than the logarithmic bound that we have established for ourselves. In proof of stake, unfortunately we do not have such a nice mechanism.

Light Clients in Proof of Stake

If we want to have an effective light client for proof of stake, ideally we would like to achieve the exact same complexity-theoretic properties as proof of work, although necessarily in a different way. Once a block header is trusted, the process for accessing any data from the header is the same, so we know that it will take a logarithmic amount of time in order to do. However, we want the process of validating the block headers themselves to be logarithmic as well.

To start off, let us describe an older version of Slasher, which was not particularly designed to be explicitly light-client friendly:

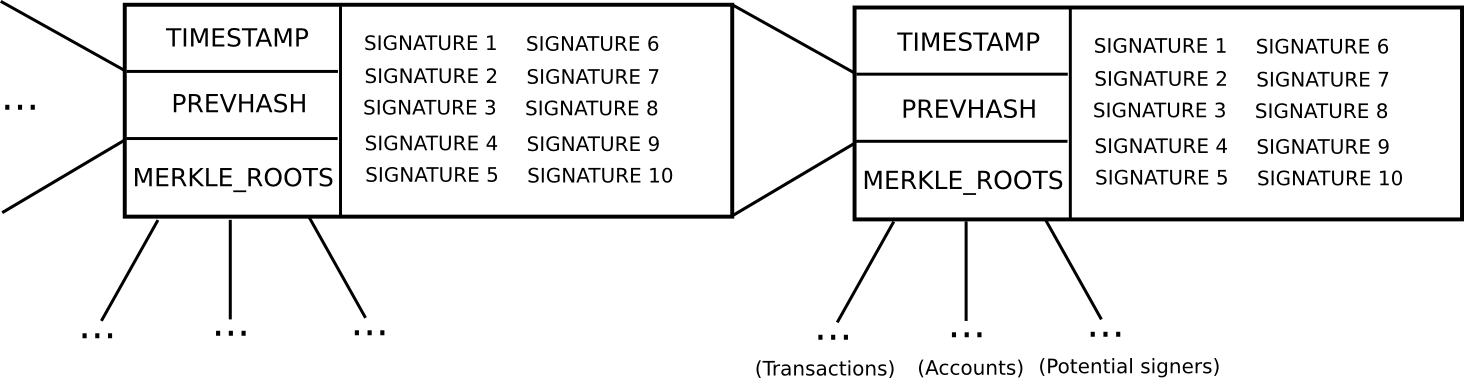
  1. In order to be a “potential blockmaker” or “potential signer”, a user must put down a security deposit of some size. This security deposit can be put down at any time, and lasts for a long period of time, say 3 months.
  2. During every time slot T (eg. T = 3069120 to 3069135 seconds after genesis), some function produces a random number R (there are many nuances behind making the random number secure, but they are not relevant here). Then, suppose that the set of potential signers ps (stored in a separate Merkle tree) has size N. We take ps[sha3(R) % N] as the blockmaker, and ps[sha3(R + 1) % N], ps[sha3(R + 2) % N] … ps[sha3(R + 15) % N] as the signers (essentially, using R as entropy to randomly select a signer and 15 blockmakers)
  3. Blocks consist of a header containing (i) the hash of the previous block, (ii) the list of signatures from the blockmaker and signers, and (iii) the Merkle root of the transactions and state, as well as (iv) auxiliary data like the timestamp.
  4. A block produced during time slot T is valid if that block is signed by the blockmaker and at least 10 of the 15 signers.
  5. If a blockmaker or signer legitimately participates in the blockmaking process, they get a small signing reward.
  6. If a blockmaker or signer signs a block that is not on the main chain, then that signature can be submitted into the main chain as “evidence” that the blockmaker or signer is trying to participate in an attack, and this leads to that blockmaker or signer losing their deposit. The evidence submitter may receive 33% of the deposit as a reward.

Unlike proof of work, where the incentive not to mine on a fork of the main chain is the opportunity cost of not getting the reward on the main chain, in proof of stake the incentive is that if you mine on the wrong chain you will get explicitly punished for it. This is important; because a very large amount of punishment can be meted out per bad signature, a much smaller number of block headers are required to achieve the same security margin.

Now, let us examine what a light client needs to do. Suppose that the light client was last online N blocks ago, and wants to authenticate the state of the current block. What does the light client need to do? If a light client already knows that a block B[k] is valid, and wants to authenticate the next block B[k+1], the steps are roughly as follows:

  1. Compute the function that produces the random value R during block B[k+1] (computable either constant or logarithmic time depending on implementation)
  2. Given R, get the public keys/addresses of the selected blockmaker and signer from the blockchain’s state tree (logarithmic time)
  3. Verify the signatures in the block header against the public keys (constant time)

And that’s it. Now, there is one gotcha. The set of potential signers may end up changing during the block, so it seems as though a light client might need to process the transactions in the block before being able to compute ps[sha3(R + k) % N]. However, we can resolve this by simply saying that it’s the potential signer set from the start of the block, or even a block 100 blocks ago, that we are selecting from.

Now, let us work out the formal security assurances that this protocol gives us. Suppose that a light client processes a set of blocks, B[1] ... B[n], such that all blocks starting from B[k + 1] are invalid. Assuming that all blocks up to B[k] are valid, and that the signer set for block B[i] is determined from block B[i - 100], this means that the light client will be able to correctly deduce the signature validity for blocks B[k + 1] ... B[k + 100]. Hence, if an attacker comes up with a set of invalid blocks that fool a light client, the light client can still be sure that the attacker will still have to pay ~1100 security deposits for the first 100 invalid blocks. For future blocks, the attacker will be able to get away with signing blocks with fake addresses, but 1100 security deposits is an assurance enough, particularly since the deposits can be variably sized and thus hold many millions of dollars of capital altogether.

Thus, even this older version of Slasher is, by our definition, light-client-friendly; we can get the same kind of security assurance as proof of work in logarithmic time.

A Better Light-Client Protocol

However, we can do significantly better than the naive algorithm above. The key insight that lets us go further is that of splitting the blockchain up into epochs. Here, let us define a more advanced version of Slasher, that we will call “epoch Slasher”. Epoch Slasher is identical to the above Slasher, except for a few other conditions:

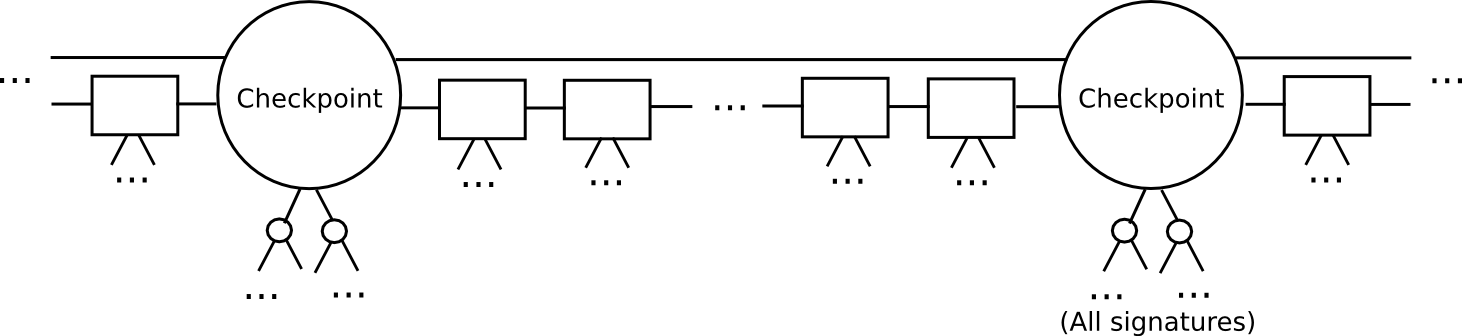
  1. Define a checkpoint as a block such that block.number % n == 0 (ie. every n blocks there is a checkpoint). Think of n as being somewhere around a few weeks long; it only needs to be substantially less than the security deposit length.
  2. For a checkpoint to be valid, 2/3 of all potential signers have to approve it. Also, the checkpoint must directly include the hash of the previous checkpoint.
  3. The set of signers during a non-checkpoint block should be determined from the set of signers during the second-last checkpoint.

This protocol allows a light client to catch up much faster. Instead of processing every block, the light client would skip directly to the next checkpoint, and validate it. The light client can even probabilistically check the signatures, picking out a random 80 signers and requesting signatures for them specifically. If the signatures are invalid, then we can be statistically certain that thousands of security deposits are going to get destroyed.

After a light client has authenticated up to the latest checkpoint, the light client can simply grab the latest block and its 100 parents, and use a simpler per-block protocol to validate them as in the original Slasher; if those blocks end up being invalid or on the wrong chain, then because the light client has already authenticated the latest checkpoint, and by the rules of the protocol it can be sure that the deposits at that checkpoint are active until at least the next checkpoint, once again the light client can be sure that at least 1100 deposits will be destroyed.

With this latter protocol, we can see that not only is proof of stake just as capable of light-client friendliness as proof of work, but moreover it’s actually even more light-client friendly. With proof of work, a light client synchronizing with the blockchain must download and process every block header in the chain, a process that is particularly expensive if the blockchain is fast, as is one of our own design objectives. With proof of stake, we can simply skip directly to the latest block, and validate the last 100 blocks before that to get an assurance that if we are on the wrong chain, at least 1100 security deposits will be destroyed.

Now, there is still a legitimate role for proof of work in proof of stake. In proof of stake, as we have seen, it takes a logarithmic amount of effort to probably-validate each individual block, and so an attacker can still cause light clients a logarithmic amount of annoyance by broadcasting bad blocks. Proof of work alone can be effectively validated in constant time, and without fetching any data from the network. Hence, it may make sense for a proof of stake algorithm to still require a small amount of proof of work on each block, ensuring that an attacker must spend some computational effort in order to even slightly inconvenience light clients. However, the amount of computational effort required to compute these proofs of work will only need to be miniscule.

The post Light Clients and Proof of Stake appeared first on .

/0 Kommentare/von

Proof of Stake: How I Learned to Love Weak Subjectivity

Proof of stake continues to be one of the most controversial discussions in the cryptocurrency space. Although the idea has many undeniable benefits, including efficiency, a larger security margin and future-proof immunity to hardware centralization concerns, proof of stake algorithms tend to be substantially more complex than proof of work-based alternatives, and there is a large amount of skepticism that proof of stake can work at all, particularly with regard to the supposedly fundamental “nothing at stake” problem. As it turns out, however, the problems are solvable, and one can make a rigorous argument that proof of stake, with all its benefits, can be made to be successful – but at a moderate cost. The purpose of this post will be to explain exactly what this cost is, and how its impact can be minimized.

Economic Sets and Nothing at Stake

First, an introduction. The purpose of a consensus algorithm, in general, is to allow for the secure updating of a state according to some specific state transition rules, where the right to perform the state transitions is distributed among some economic set. An economic set is a set of users which can be given the right to collectively perform transitions via some algorithm, and the important property that the economic set used for consensus needs to have is that it must be securely decentralized – meaning that no single actor, or colluding set of actors, can take up the majority of the set, even if the actor has a fairly large amount of capital and financial incentive. So far, we know of three securely decentralized economic sets, and each economic set corresponds to a set of consensus algorithms:

  • Owners of computing power: standard proof of work, or TaPoW. Note that this comes in specialized hardware, and (hopefully) general-purpose hardware variants.
  • Stakeholders: all of the many variants of proof of stake
  • A user’s social network: Ripple/Stellar-style consensus

Note that there have been some recent attempts to develop consensus algorithms based on traditional Byzantine fault tolerance theory; however, all such approaches are based on an M-of-N security model, and the concept of “Byzantine fault tolerance” by itself still leaves open the question of which set the N should be sampled from. In most cases, the set used is stakeholders, so we will treat such neo-BFT paradigms are simply being clever subcategories of “proof of stake”.

Proof of work has a nice property that makes it much simpler to design effective algorithms for it: participation in the economic set requires the consumption of a resource external to the system. This means that, when contributing one’s work to the blockchain, a miner must make the choice of which of all possible forks to contribute to (or whether to try to start a new fork), and the different options are mutually exclusive. Double-voting, including double-voting where the second vote is made many years after the first, is unprofitablem since it requires you to split your mining power among the different votes; the dominant strategy is always to put your mining power exclusively on the fork that you think is most likely to win.

With proof of stake, however, the situation is different. Although inclusion into the economic set may be costly (although as we will see it not always is), voting is free. This means that “naive proof of stake” algorithms, which simply try to copy proof of work by making every coin a “simulated mining rig” with a certain chance per second of making the account that owns it usable for signing a block, have a fatal flaw: if there are multiple forks, the optimal strategy is to vote on all forks at once. This is the core of “nothing at stake”.

Note that there is one argument for why it might not make sense for a user to vote on one fork in a proof-of-stake environment: “altruism-prime”. Altruism-prime is essentially the combination of actual altruism (on the part of users or software developers), expressed both as a direct concern for the welfare of others and the network and a psychological moral disincentive against doing something that is obviously evil (double-voting), as well as the “fake altruism” that occurs because holders of coins have a desire not to see the value of their coins go down.

Unfortunately, altruism-prime cannot be relied on exclusively, because the value of coins arising from protocol integrity is a public good and will thus be undersupplied (eg. if there are 1000 stakeholders, and each of their activity has a 1% chance of being “pivotal” in contributing to a successful attack that will knock coin value down to zero, then each stakeholder will accept a bribe equal to only 1% of their holdings). In the case of a distribution equivalent to the Ethereum genesis block, depending on how you estimate the probability of each user being pivotal, the required quantity of bribes would be equal to somewhere between 0.3% and 8.6% of total stake (or even less if an attack is nonfatal to the currency). However, altruism-prime is still an important concept that algorithm designers should keep in mind, so as to take maximal advantage of in case it works well.

Short and Long Range

If we focus our attention specifically on short-range forks – forks lasting less than some number of blocks, perhaps 3000, then there actually is a solution to the nothing at stake problem: security deposits. In order to be eligible to receive a reward for voting on a block, the user must put down a security deposit, and if the user is caught either voting on multiple forks then a proof of that transaction can be put into the original chain, taking the reward away. Hence, voting for only a single fork once again becomes the dominant strategy.

Another set of strategies, called “Slasher 2.0″ (in contrast to Slasher 1.0, the original security deposit-based proof of stake algorithm), involves simply penalizing voters that vote on the wrong fork, not voters that double-vote. This makes analysis substantially simpler, as it removes the need to pre-select voters many blocks in advance to prevent probabilistic double-voting strategies, although it does have the cost that users may be unwilling to sign anything if there are two alternatives of a block at a given height. If we want to give users the option to sign in such circumstances, a variant of logarithmic scoring rules can be used (see here for more detailed investigation). For the purposes of this discussion, Slasher 1.0 and Slasher 2.0 have identical properties.

The reason why this only works for short-range forks is simple: the user has to have the right to withdraw the security deposit eventually, and once the deposit is withdrawn there is no longer any incentive not to vote on a long-range fork starting far back in time using those coins. One class of strategies that attempt to deal with this is making the deposit permanent, but these approaches have a problem of their own: unless the value of a coin constantly grows so as to continually admit new signers, the consensus set ends up ossifying into a sort of permanent nobility. Given that one of the main ideological grievances that has led to cryptocurrency’s popularity is precisely the fact that centralization tends to ossify into nobilities that retain permanent power, copying such a property will likely be unacceptable to most users, at least for blockchains that are meant to be permanent. A nobility model may well be precisely the correct approach for special-purpose ephemeral blockchains that are meant to die quickly (eg. one might imagine such a blockchain existing for a round of a blockchain-based game).

One class of approaches at solving the problem is to combine the Slasher mechanism described above for short-range forks with a backup, transactions-as-proof-of-stake, for long range forks. TaPoS essentially works by counting transaction fees as part of a block’s “score” (and requiring every transaction to include some bytes of a recent block hash to make transactions not trivially transferable), the theory being that a successful attack fork must spend a large quantity of fees catching up. However, this hybrid approach has a fundamental flaw: if we assume that the probability of an attack succeeding is near-zero, then every signer has an incentive to offer a service of re-signing all of their transactions onto a new blockchain in exchange for a small fee; hence, a zero probability of attacks succeeding is not game-theoretically stable. Does every user setting up their own node.js webapp to accept bribes sound unrealistic? Well, if so, there’s a much easier way of doing it: sell old, no-longer-used, private keys on the black market. Even without black markets, a proof of stake system would forever be under the threat of the individuals that originally participated in the pre-sale and had a share of genesis block issuance eventually finding each other and coming together to launch a fork.

Because of all the arguments above, we can safely conclude that this threat of an attacker building up a fork from arbitrarily long range is unfortunately fundamental, and in all non-degenerate implementations the issue is fatal to a proof of stake algorithm’s success in the proof of work security model. However, we can get around this fundamental barrier with a slight, but nevertheless fundamental, change in the security model.

Weak Subjectivity

Although there are many ways to categorize consensus algorithms, the division that we will focus on for the rest of this discussion is the following. First, we will provide the two most common paradigms today:

  • Objective: a new node coming onto the network with no knowledge except (i) the protocol definition and (ii) the set of all blocks and other “important” messages that have been published can independently come to the exact same conclusion as the rest of the network on the current state.
  • Subjective: the system has stable states where different nodes come to different conclusions, and a large amount of social information (ie. reputation) is required in order to participate.

Systems that use social networks as their consensus set (eg. Ripple) are all necessarily subjective; a new node that knows nothing but the protocol and the data can be convinced by an attacker that their 100000 nodes are trustworthy, and without reputation there is no way to deal with that attack. Proof of work, on the other hand, is objective: the current state is always the state that contains the highest expected amount of proof of work.

Now, for proof of stake, we will add a third paradigm:

  • Weakly subjective: a new node coming onto the network with no knowledge except (i) the protocol definition, (ii) the set of all blocks and other “important” messages that have been published and (iii) a state from less than N blocks ago that is known to be valid can independently come to the exact same conclusion as the rest of the network on the current state, unless there is an attacker that permanently has more than X percent control over the consensus set.

Under this model, we can clearly see how proof of stake works perfectly fine: we simply forbid nodes from reverting more than N blocks, and set N to be the security deposit length. That is to say, if state S has been valid and has become an ancestor of at least N valid states, then from that point on no state S’ which is not a descendant of S can be valid. Long-range attacks are no longer a problem, for the trivial reason that we have simply said that long-range forks are invalid as part of the protocol definition. This rule clearly is weakly subjective, with the added bonus that X = 100% (ie. no attack can cause permanent disruption unless it lasts more than N blocks).

Another weakly subjective scoring method is exponential subjective scoring, defined as follows:

  1. Every state S maintains a “score” and a “gravity”
  2. score(genesis) = 0, gravity(genesis) = 1
  3. score(block) = score(block.parent) + weight(block) * gravity(block.parent), where weight(block) is usually 1, though more advanced weight functions can also be used (eg. in Bitcoin, weight(block) = block.difficulty can work well)
  4. If a node sees a new block B' with B as parent, then if n is the length of the longest chain of descendants from B at that time, gravity(B') = gravity(B) * 0.99 ^ n (note that values other than 0.99 can also be used).

Essentially, we explicitly penalize forks that come later. ESS has the property that, unlike more naive approaches at subjectivity, it mostly avoids permanent network splits; if the time between the first node on the network hearing about block B and the last node on the network hearing about block B is an interval of k blocks, then a fork is unsustainable unless the lengths of the two forks remain forever within roughly k percent of each other (if that is the case, then the differing gravities of the forks will ensure that half of the network will forever see one fork as higher-scoring and the other half will support the other fork). Hence, ESS is weakly subjective with X roughly corresponding to how close to a 50/50 network split the attacker can create (eg. if the attacker can create a 70/30 split, then X = 0.29).

In general, the “max revert N blocks” rule is superior and less complex, but ESS may prove to make more sense in situations where users are fine with high degrees of subjectivity (ie. N being small) in exchange for a rapid ascent to very high degrees of security (ie. immune to a 99% attack after N blocks).

Consequences

So what would a world powered by weakly subjective consensus look like? First of all, nodes that are always online would be fine; in those cases weak subjectivity is by definition equivalent to objectivity. Nodes that pop online once in a while, or at least once every N blocks, would also be fine, because they would be able to constantly get an updated state of the network. However, new nodes joining the network, and nodes that appear online after a very long time, would not have the consensus algorithm reliably protecting them. Fortunately, for them, the solution is simple: the first time they sign up, and every time they stay offline for a very very long time, they need only get a recent block hash from a friend, a blockchain explorer, or simply their software provider, and paste it into their blockchain client as a “checkpoint”. They will then be able to securely update their view of the current state from there.

This security assumption, the idea of “getting a block hash from a friend”, may seem unrigorous to many; Bitcoin developers often make the point that if the solution to long-range attacks is some alternative deciding mechanism X, then the security of the blockchain ultimately depends on X, and so the algorithm is in reality no more secure than using X directly – implying that most X, including our social-consensus-driven approach, are insecure.

However, this logic ignores why consensus algorithms exist in the first place. Consensus is a social process, and human beings are fairly good at engaging in consensus on our own without any help from algorithms; perhaps the best example is the Rai stones, where a tribe in Yap essentially maintained a blockchain recording changes to the ownership of stones (used as a Bitcoin-like zero-intrinsic-value asset) as part of its collective memory. The reason why consensus algorithms are needed is, quite simply, because humans do not have infinite computational power, and prefer to rely on software agents to maintain consensus for us. Software agents are very smart, in the sense that they can maintain consensus on extremely large states with extremely complex rulesets with perfect precision, but they are also very ignorant, in the sense that they have very little social information, and the challenge of consensus algorithms is that of creating an algorithm that requires as little input of social information as possible.

Weak subjectivity is exactly the correct solution. It solves the long-range problems with proof of stake by relying on human-driven social information, but leaves to a consensus algorithm the role of increasing the speed of consensus from many weeks to twelve seconds and of allowing the use of highly complex rulesets and a large state. The role of human-driven consensus is relegated to maintaining consensus on block hashes over long periods of time, something which people are perfectly good at. A hypothetical oppressive government which is powerful enough to actually cause confusion over the true value of a block hash from one year ago would also be powerful enough to overpower any proof of work algorithm, or cause confusion about the rules of blockchain protocol.

Note that we do not need to fix N; theoretically, we can come up with an algorithm that allows users to keep their deposits locked down for longer than N blocks, and users can then take advantage of those deposits to get a much more fine-grained reading of their security level. For example, if a user has not logged in since T blocks ago, and 23% of deposits have term length greater than T, then the user can come up with their own subjective scoring function that ignores signatures with newer deposits, and thereby be secure against attacks with up to 11.5% of total stake. An increasing interest rate curve can be used to incentivize longer-term deposits over shorter ones, or for simplicity we can just rely on altruism-prime.

Marginal Cost: The Other Objection

One objection to long-term deposits is that it incentivizes users keeping their capital locked up, which is inefficient, the exact same problem as proof of work. However, there are three counterpoints to this. First, marginal cost is not total cost, and the ratio of total cost divided by marginal cost is much less for proof of stake than proof of work.

A user will likely experience close to no pain from locking up 50% of their capital for a few months, a slight amount of pain from locking up 70%, but would find locking up more than 85% intolerable without a large reward. Additionally, different users have very different preferences for how willing they are to lock up capital. Because of these two factors put together, regardless of what the equilibrium interest rate ends up being the vast majority of the capital will be locked up at far below marginal cost.

Fortunately, there is a way to test those assumptions: launch a proof of stake coin with a stake reward of 1%, 2%, 3%, etc per year, and see just how large a percentage of coins become deposits in each case. Users will not act against their own interests, so we can simply use the quantity of funds spent on consensus as a proxy for how much inefficiency the consensus algorithm introduces; if proof of stake has a reasonable level of security at a much lower reward level than proof of work, then we know that proof of stake is a more efficient consensus mechanism, and we can use the levels of participation at different reward levels to get an accurate idea of the ratio between total cost and marginal cost. Ultimately, it may take years to get an exact idea of just how large these costs are.

Second, locking up capital is a private cost, but an equally strong public good. The presence of locked up capital means that there is less money supply available for transactional purposes, and so the value of the currency will increase, redistributing the capital to everyone else. Third, security deposits are a very safe store of value, so (i) they substitute the use of money as a personal crisis insurance tool, and (ii) many users will be able to take out loans in the same currency collateralized by the security deposit.

As a conclusion, we now know for certain that (i) proof of stake algorithms can be made secure, and weak subjectivity is both sufficient and necessary as a fundamental change in the security model to sidestep nothing-at-stake concerns, and (ii) there are substantial economic reasons to believe that proof of stake actually is much more economically efficient than proof of work. Proof of stake is not an unknown; the past six months of formalization and research have determined exactly where the strengths and weaknesses lie, at least to as large extent as with proof of work, where mining centralization uncertainties may well forever abound. Now, it’s simply a matter of standardizing the algorithms, and giving blockchain developers the choice.

The post Proof of Stake: How I Learned to Love Weak Subjectivity appeared first on ethereum blog.

ethereum blog

/0 Kommentare/von

Slasher Ghost, and Other Developments in Proof of Stake

Special thanks to Vlad Zamfir and Zack Hess for ongoing research and discussions on proof-of-stake algorithms and their own input into Slasher-like proposals

One of the hardest problems in cryptocurrency development is that of devising effective consensus algorithms. Certainly, relatively passable default options exist. At the very least it is possible to rely on a Bitcoin-like proof of work algorithm based on either a randomly-generated circuit approach targeted for specialized-hardware resitance, or failing that simple SHA3, and our existing GHOST optimizations allow for such an algorithm to provide block times of 12 seconds. However, proof of work as a general category has many flaws that call into question its sustainability as an exclusive source of consensus; 51% attacks from altcoin miners, eventual ASIC dominance and high energy inefficiency are perhaps the most prominent. Over the last few months we have become more and more convinced that some inclusion of proof of stake is a necessary component for long-term sustainability; however, actually implementing a proof of stake algorithm that is effective is proving to be surprisingly complex.

The fact that Ethereum includes a Turing-complete contracting system complicates things further, as it makes certain kinds of collusion much easier without requiring trust, and creates a large pool of stake in the hands of decentralized entities that have the incentive to vote with the stake to collect rewards, but which are too stupid to tell good blockchains from bad. What the rest of this article will show is a set of strategies that deal with most of the issues surrounding proof of stake algorithms as they exist today, and a sketch of how to extend our current preferred proof-of-stake algorithm, Slasher, into something much more robust.

Historical Overview: Proof of stake and Slasher

If you’re not yet well-versed in the nuances of proof of stake algorithms, first read: https://blog.ethereum.org/2014/07/05/stake/

The fundamental problem that consensus protocols try to solve is that of creating a mechanism for growing a blockchain over time in a decentralized way that cannot easily be subverted by attackers. If a blockchain does not use a consensus protocol to regulate block creation, and simply allows anyone to add a block at any time, then an attacker or botnet with very many IP addresses could flood the network with blocks, and particularly they can use their power to perform double-spend attacks – sending a payment for a product, waiting for the payment to be confirmed in the blockchain, and then starting their own “fork” of the blockchain, substituting the payment that they made earlier with a payment to a different account controlled by themselves, and growing it longer than the original so everyone accepts this new blockchain without the payment as truth.

The general solution to this problem involves making a block “hard” to create in some fashion. In the case of proof of work, each block requires computational effort to produce, and in the case of proof of stake it requires ownership of coins – in most cases, it’s a probabilistic process where block-making privileges are doled out randomly in proportion to coin holdings, and in more exotic “negative block reward” schemes anyone can create a block by spending a certain quantity of funds, and they are compensated via transaction fees. In any of these approaches, each chain has a “score” that roughly reflects the total difficulty of producing the chain, and the highest-scoring chain is taken to represent the “truth” at that particular time.

For a detailed overview of some of the finer points of proof of stake, see the above-linked article; for those readers who are already aware of the issues I will start off by presenting a semi-formal specification for Slasher:

  1. Blocks are produced by miners; in order for a block to be valid it must satisfy a proof-of-work condition. However, this condition is relatively weak (eg. we can target the mining reward to something like 0.02x the genesis supply every year)
  2. Every block has a set of designated signers, which are chosen beforehand (see below). For a block with valid PoW to be accepted as part of the chain it must be accompanied by signatures from at least two thirds of its designated signers.
  3. When block N is produced, we say that the set of potential signers of block N + 3000 is the set of addresses such that sha3(address + block[N].hash) < block[N].balance(address) * D2 where D2 is a difficulty parameter targeting 15 signers per block (ie. if block N has less than 15 signers it goes down otherwise it goes up). Note that the set of potential signers is very computationally intensive to fully enumerate, and we don’t try to do so; instead we rely on signers to self-declare.
  4. If a potential signer for block N + 3000 wants to become a designated signer for that block, they must send a special transaction accepting this responsibility and that transaction must get included between blocks N + 1 and N + 64. The set of designated signers for block N + 3000 is the set of all individuals that do this. This “signer must confirm” mechanism helps ensure that the majority of signers will actually be online when the time comes to sign. For blocks 0 … 2999, the set of signers is empty, so proof of work alone suffices to create those blocks.
  5. When a designated signer adds their signature to block N + 3000, they are scheduled to receive a reward in block N + 6000.
  6. If a signer signs two different blocks at height N + 3000, then if someone detects the double-signing before block N + 6000 they can submit an “evidence” transaction containing the two signatures, destroying the signer’s reward and transferring a third of it to the whistleblower.
  7. If there is an insufficient number of signers to sign at a particular block height h, a miner can produce a block with height h+1 directly on top of the block with height h-1 by mining at an 8x higher difficulty (to incentivize this, but still make it less attractive than trying to create a normal block, there is a 6x higher reward). Skipping over two blocks has higher factors of 16x diff and 12x reward, three blocks 32x and 24x, etc.

Essentially, by explicitly punishing double-signing, Slasher in a lot of ways, although not all, makes proof of stake act like a sort of simulated proof of work. An important incidental benefit of Slasher is the non-revert property. In proof of work, sometimes after one node mines one block some other node will immediately mine two blocks, and so some nodes will need to revert back one block upon seeing the longer chain. Here, every block requires two thirds of the signers to ratify it, and a signer cannot ratify two blocks at the same height without losing their gains in both chains, so assuming no malfeasance the blockchain will never revert. From the point of view of a decentralized application developer, this is a very desirable property as it means that “time” only moves in one direction, just like in a server-based environment.

However, Slasher is still vulnerable to one particular class of attack: long-range attacks. Instead of trying to start a fork from ten blocks behind the current head, suppose that an attacker tries to start a fork starting from ten thousand blocks behind, or even the genesis block – all that matters is that the depth of the fork must be greater than the duration of the reward lockup. At that point, because users’ funds are unlocked and they can move them to a new address to escape punishment, users have no disincentive against signing on both chains. In fact, we may even expect to see a black market of people selling their old private keys, culminating with an attacker single-handedly acquiring access to the keys that controlled over 50% of the currency supply at some point in history.

One approach to solving the long-range double-signing problem is transactions-as-proof-of-stake, an alternative PoS solution that does not have an incentive to double-sign because it’s the transactions that vote, and there is no reward for sending a transaction (in fact there’s a cost, and the reward is outside the network); however, this does nothing to stop the black key market problem. To properly deal with that issue, we will need to relax a hidden assumption.

Subjective Scoring and Trust

For all its faults, proof of work does have some elegant economic properties. Particularly, because proof of work requires an externally rivalrous resource, something with exists and is consumed outside the blockchain, in order to generate blocks (namely, computational effort), launching a fork against a proof of work chain invariably requires having access to, and spending, a large quantity of economic resources. In the case of proof of stake, on the other hand, the only scarce value involved is value within the chain, and between multiple chains that value is not scarce at all. No matter what algorithm is used, in proof of stake 51% of the owners of the genesis block could eventually come together, collude, and produce a longer (ie. higher-scoring) chain than everyone else.

This may seem like a fatal flaw, but in reality it is only a flaw if we implicitly accept an assumption that is made in the case of proof of work: that nodes have no knowledge of history. In a proof-of-work protocol, a new node, having no direct knowledge of past events and seeing nothing but the protocol source code and the set of messages that have already been published, can join the network at any point and determine the score of all possible chains, and from there the block that is at the top of the highest-scoring main chain. With proof of stake, as we described, such a property cannot be achieved, since it’s very cheap to acquire historical keys and simulate alternate histories. Thus, we will relax our assumptions somewhat: we will say that we are only concerned with maintaining consensus between a static set of nodes that are online at least once every N days, allowing these nodes to use their own knowledge of history to reject obvious long-range forks using some formula, and new nodes or long-dormant nodes will need to specify a “checkpoint” (a hash of a block representing what the rest of the network agrees is a recent state) in order to get back onto the consensus.

Such an approach is essentially a hybrid between the pure and perhaps harsh trust-no-one logic of Bitcoin and the total dependency on socially-driven consensus found in networks like Ripple. In Ripple’s case, users joining the system need to select a set of nodes that they trust (or, more precisely, trust not to collude) and rely on those nodes during every step of the consensus process. In the case of Bitcoin, the theory is that no such trust is required and the protocol is completely self-contained; the system works just as well between a thousand isolated cavemen with laptops on a thousand islands as it does in a strongly connected society (in fact, it might work better with island cavemen, since without trust collusion is more difficult). In our hybrid scheme, users need only look to the society outside of the protocol exactly once – when they first download a client and find a checkpoint – and can enjoy Bitcoin-like trust properties starting from that point.

In order to determine which trust assumption is the better one to take, we ultimately need to ask a somewhat philosophical question: do we want our consensus protocols to exist as absolute cryptoeconomic constructs completely independent of the outside world, or are we okay with relying heavily on the fact that these systems exist in the context of a wider society? Although it is indeed a central tenet of mainstream cryptocurrency philosophy that too much external dependence is dangerous, arguably the level of independence that Bitcoin affords us in reality is no greater than that provided by the hybrid model. The argument is simple: even in the case of Bitcoin, a user must also take a leap of trust upon joining the network – first by trusting that they are joining a protocol that contains assets that other people find valuable (eg. how does a user know that bitcoins are worth $ 380 each and dogecoins only $ 0.0004? Especially with the different capabilities of ASICs for different algorithms, hashpower is only a very rough estimate), and second by trusting that they are downloading the correct software package. In both the supposedly “pure” model and the hybrid model there is always a need to look outside the protocol exactly once. Thus, on the whole, the gain from accepting the extra trust requirement (namely, environmental friendliness and security against oligopolistic mining pools and ASIC farms) is arguably worth the cost.

Additionally, we may note that, unlike Ripple consensus, the hybrid model is still compatible with the idea of blockchains “talking” to each each other by containing a minimal “light” implementation of each other’s protocols. The reason is that, while the scoring mechanism is not “absolute” from the point of view of a node without history suddenly looking at every block, it is perfectly sufficient from the point of view of an entity that remains online over a long period of time, and a blockchain certainly is such an entity.

So far, there have been two major approaches that followed some kind of checkpoint-based trust model:

  1. Developer-issued checkpoints – the client developer issues a new checkpoint with each client upgrade (eg. used in PPCoin)
  2. Revert limit – nodes refuse to accept forks that revert more than N (eg. 3000) blocks (eg. used in Tendermint)

The first approach has been roundly criticized by the cryptocurrency community for being too centralized. The second, however, also has a flaw: a powerful attacker can not only revert a few thousand blocks, but also potentially split the network permanently. In the N-block revert case, the strategy is as follows. Suppose that the network is currently at block 10000, and N = 3000. The attacker starts a secret fork, and grows it by 3001 blocks faster than the main network. When the main network gets to 12999, and some node produces block 13000, the attacker reveals his own fork. Some nodes will see the main network’s block 13000, and refuse to switch to the attacker’s fork, but the nodes that did not yet see that block will be happy to revert from 12999 to 10000 and then accept the attacker’s fork. From there, the network is permanently split.

Fortunately, one can actually construct a third approach that neatly solves this problem, which we will call exponentially subjective scoring. Essentially, instead of rejecting forks that go back too far, we simply penalize them on a graduating scale. For every block, a node maintains a score and a “gravity” factor, which acts as a multiplier to the contribution that the block makes to the blockchain’s score. The gravity of the genesis block is 1, and normally the gravity of any other block is set to be equal to the gravity of its parent. However, if a node receives a block whose parent already has a chain of N descendants (ie. it’s a fork reverting N blocks), that block’s gravity is penalized by a factor of 0.99N, and the penalty propagates forever down the chain and stacks multiplicatively with other penalties.

That is, a fork which starts 1 block ago will need to grow 1% faster than the main chain in order to overtake it, a fork which starts 100 blocks ago will need to grow 2.718 times as quickly, and a fork which starts 3000 blocks ago will need to grow 12428428189813 times as quickly – clearly an impossibility with even trivial proof of work.

The algorithm serves to smooth out the role of checkpointing, assigning a small “weak checkpoint” role to each individual block. If an attacker produces a fork that some nodes hear about even three blocks earlier than others, those two chains will need to stay within 3% of each other forever in order for a network split to maintain itself.

There are other solutions that could be used aside from, or even alongside ESS; a particular set of strategies involves stakeholders voting on a checkpoint every few thousand blocks, requiring every checkpoint produced to reflect a large consensus of the majority of the current stake (the reason the majority of the stake can’t vote on every block is, of course, that having that many signatures would bloat the blockchain).

Slasher Ghost

The other large complexity in implementing proof of stake for Ethereum specifically is the fact that the network includes a Turing-complete financial system where accounts can have arbitrary permissions and even permissions that change over time. In a simple currency, proof of stake is relatively easy to accomplish because each unit of currency has an unambiguous owner outside the system, and that owner can be counted on to participate in the stake-voting process by signing a message with the private key that owns the coins. In Ethereum, however, things are not quite so simple: if we do our job promoting proper wallet security right, the majority of ether is going to be stored in specialized storage contracts, and with Turing-complete code there is no clear way of ascertaining or assigning an “owner”.

One strategy that we looked at was delegation: requiring every address or contract to assign an address as a delegate to sign for them, and that delegate account would have to be controlled by a private key. However, there is a problem with any such approach. Suppose that a majority of the ether in the system is actually stored in application contracts (as opposed to personal storage contracts); this includes deposits in SchellingCoins and other stake-based protocols, security deposits in probabilistic enforcement systems, collateral for financial derivatives, funds owned by DAOs, etc. Those contracts do not have an owner even in spirit; in that case, the fear is that the contract will default to a strategy of renting out stake-voting delegations to the highest bidder. Because attackers are the only entities willing to bid more than the expected return from the delegation, this will make it very cheap for an attacker to acquire the signing rights to large quantities of stake.

The only solution to this within the delegation paradigm is to make it extremely risky to dole out signing privileges to untrusted parties; the simplest approach is to modify Slasher to require a large deposit, and slash the deposit as well as the reward in the event of double-signing. However, if we do this then we are essentially back to entrusting the fate of a large quantity of funds to a single private key, thereby defeating much of the point of Ethereum in the first place.

Fortunately, there is one alternative to delegation that is somewhat more effective: letting contracts themselves sign. To see how this works, consider the following protocol:

  1. There is now a SIGN opcode added.
  2. A signature is a series of virtual transactions which, when sequentially applied to the state at the end of the parent block, results in the SIGN opcode being called. The nonce of the first VTX in the signature must be the prevhash being signed, the nonce of the second must be the prevhash plus one, and so forth (alternatively, we can make the nonces -1, -2, -3 etc. and require the prevhash to be passed in through transaction data so as to be eventually supplied as an input to the SIGN opcode).
  3. When the block is processed, the state transitions from the VTXs are reverted (this is what is meant by “virtual”) but a deposit is subtracted from each signing contract and the contract is registered to receive the deposit and reward in 3000 blocks.

Basically, it is the contract’s job to determine the access policy for signing, and the contract does this by placing the SIGN opcode behind the appropriate set of conditional clauses. A signature now becomes a set of transactions which together satisfy this access policy. The incentive for contract developers to keep this policy secure, and not dole it out to anyone who asks, is that if it is not secure then someone can double-sign with it and destroy the signing deposit, taking a portion for themselves as per the Slasher protocol. Some contracts will still delegate, but this is unavoidable; even in proof-of-stake systems for plain currencies such as NXT, many users end up delegating (eg. DPOS even goes so far as to institutionalize delegation), and at least here contracts have an incentive to delegate to an access policy that is not likely to come under the influence of a hostile entity – in fact, we may even see an equilibrium where contracts compete to deliver secure blockchain-based stake pools that are least likely to double-vote, thereby increasing security over time.

However, the virtual-transactions-as-signatures paradigm does impose one complication: it is no longer trivial to provide an evidence transaction showing two signatures by the same signer at the same block height. Because the result of a transaction execution depends on the starting state, in order to ascertain whether a given evidence transaction is valid one must prove everything up to the block in which the second signature was given. Thus, one must essentially “include” the fork of a blockchain inside of the main chain. To do this efficiently, a relatively simple proposal is a sort of “Slasher GHOST” protocol, where one can include side-blocks in the main chain as uncles. Specifically, we declare two new transaction types:

  1. [block_number, uncle_hash] – this transaction is valid if (1) the block with the given uncle_hash has already been validated, (2) the block with the given uncle_hash has the given block number, and (3) the parent of that uncle is either in the main chain or was included earlier as an uncle. During the act of processing this transaction, if addresses that double-signed at that height are detected, they are appropriately penalized.
  2. [block_number, uncle_parent_hash, vtx] – this transaction is valid if (1) the block with the given uncle_parent_hash has already been validated, (2) the given virtual transaction is valid at the given block height with the state at the end of uncle_parent_hash, and (3) the virtual transaction shows a signature by an address which also signed a block at the given block_number in the main chain. This transaction penalizes that one address.

Essentially, one can think of the mechanism as working like a “zipper”, with one block from the fork chain at a time being zipped into the main chain. Note that for a fork to start, there must exist double-signers at every block; there is no situation where there is a double-signer 1500 blocks into a fork so a whistleblower must “zip” 1499 innocent blocks into a chain before getting to the target block – rather, in such a case, even if 1500 blocks need to be added, each one of them notifies the main chain about five separate malfeasors that double-signed at that height. One somewhat complicated property of the scheme is that the validity of these “Slasher uncles” depends on whether or not the node has validated a particular block outside of the main chain; to facilitate this, we specify that a response to a “getblock” message in the wire protocol must include the uncle-dependencies for a block before the actual block. Note that this may sometimes lead to a recursive expansion; however, the denial-of-service potential is limited since each individual block still requires a substantial quantity of proof-of-work to produce.

Blockmakers and Overrides

Finally, there is a third complication. In the hybrid-proof-of-stake version of Slasher, if a miner has an overwhelming share of the hashpower, then the miner can produce multiple versions of each block, and send different versions to different parts of the network. Half the signers will see and sign one block, half will see and sign another block, and the network will be stuck with two blocks with insufficient signatures, and no signer willing to slash themselves to complete the process; thus, a proof-of-work override will be required, a dangerous situation since the miner controls most of the proof-of-work. There are two possible solutions here:

  1. Signers should wait a few seconds after receiving a block before signing, and only sign stochastically in some fashion that ensures that a random one of the blocks will dominate.
  2. There should be a single “blockmaker” among the signers whose signature is required for a block to be valid. Effectively, this transfers the “leadership” role from a miner to a stakeholder, eliminating the problem, but at the cost of adding a dependency on a single party that now has the ability to substantially inconvenience everyone by not signing, or unintentionally by being the target of a denial-of-service attack. Such behavior can be disincentivized by having the signer lose part of their deposit if they do not sign, but even still this will result in a rather jumpy block time if the only way to get around an absent blockmaker is using a proof-of-work override.

One possible solution to the problem in (2) is to remove proof of work entirely (or almost entirely, keeping a minimal amount for anti-DDoS value), replacing it with a mechanism that Vlad Zamfir has coined “delegated timestamping”. Essentially, every block must appear on schedule (eg. at 15 second intervals), and when a block appears the signers vote 1 if the block was on time, or 0 if the block was too early or too late. If the majority of the signers votes 0, then the block is treated as invalid – kept in the chain in order to give the signers their fair reward, but the blockmaker gets no reward and the state transition gets skipped over. Voting is incentivized via schellingcoin – the signers whose vote agrees with the majority get an extra reward, so assuming that everyone else is going to be honest everyone has the incentive to be honest, in a self-reinforcing equilibrium. The theory is that a 15-second block time is too fast for signers to coordinate on a false vote (the astute reader may note that the signers were decided 3000 blocks in advance so this is not really true; to fix this we can create two groups of signers, one pre-chosen group for validation and another group chosen at block creation time for timestamp voting).

Putting it all Together

Taken together, we can thus see something like the following working as a functional version of Slasher:

  1. Every block has a designated blockmaker, a set of designated signers, and a set of designated timestampers. For a block to be accepted as part of the chain it must be accompanied by virtual-transactions-as-signatures from the blockmaker, two thirds of the signers and 10 timestampers, and the block must have some minimal proof of work for anti-DDoS reasons (say, targeted to 0.01x per year)
  2. During block N, we say that the set of potential signers of block N + 3000 is the set of addresses such that sha3(address + block[N].hash) < block[N].balance(address) * D2 where D2 is a difficulty parameter targeting 15 signers per block (ie. if block N has less than 15 signers it goes down otherwise it goes up).
  3. If a potential signer for block N + 3000 wants to become a signer, they must send a special transaction accepting this responsibility and supplying a deposit, and that transaction must get included between blocks N + 1 and N + 64. The set of designated signers for block N + 3000 is the set of all individuals that do this, and the blockmaker is the designated signer with the lowest value for sha3(address + block[N].hash). If the signer set is empty, no block at that height can be made. For blocks 0 … 2999, the blockmaker and only signer is the protocol developer.
  4. The set of timestampers of the block N + 3000 is the set of addresses such that sha3(address + block[N].hash) < block[N].balance(address) * D3, where D3 is targeted such that there is an average of 20 timestampers each block (ie. if block N has less than 20 timestampers it goes down otherwise it goes up).
  5. Let T be the timestamp of the genesis block. When block N + 3000 is released, timestampers can supply virtual-transactions-as-signatures for that block, and have the choice of voting 0 or 1 on the block. Voting 1 means that they saw the block within 7.5 seconds of time T + (N + 3000) * 15, and voting 0 means that they received the block when the time was outside that range. Note that nodes should detect if their clocks are out of sync with everyone else’s clocks on the blockchain, and if so adjust their system clocks.
  6. Timestampers who voted along with the majority receive a reward, other timestampers get nothing.
  7. The designated signers for block N + 3000 have the ability to sign that block by supplying a set of virtual-transactions-as-a-signature. All designated signers who sign are scheduled to receive a reward and their returned deposit in block N + 6000. Signers who skipped out are scheduled to receive their returned deposit minus twice the reward (this means that it’s only economically profitable to sign up as a signer if you actually think there is a chance greater than 2/3 that you will be online).
  8. If the majority timestamper vote is 1, the blockmaker is scheduled to receive a reward and their returned deposit in block N + 6000. If the majority timestamper vote is 0, the blockmaker is scheduled to receive their deposit minus twice the reward, and the block is ignored (ie. the block is in the chain, but it does not contribute to the chain’s score, and the state of the next block starts from the end state of the block before the rejected block).
  9. If a signer signs two different blocks at height N + 3000, then if someone detects the double-signing before block N + 6000 they can submit an “evidence” transaction containing the two signatures to either or both chains, destroying the signer’s reward and deposit and transferring a third of it to the whistleblower.
  10. If there is an insufficient number of signers to sign or the blockmaker is missing at a particular block height h, the designated blockmaker for height h + 1 can produce a block directly on top of the block at height h - 1 after waiting for 30 seconds instead of 15.

After years of research, one thing has become clear: proof of stake is non-trivial – so non-trivial that some even consider it impossible. The issues of nothing-at-stake and long-range attacks, and the lack of mining as a rate-limiting device, require a number of compensatory mechanisms, and even the protocol above does not address the issue of how to randomly select signers. With a substantial proof of work reward, the problem is limited, as block hashes can be a source of randomness and we can mathematically show that the gain from holding back block hashes until a miner finds a hash that favorably selects future signers is usually less than the gain from publishing the block hashes. Without such a reward, however, other sources of randomness such as low-influence functions need to be used.

For Ethereum 1.0, we consider it highly desirable to both not excessively delay the release and not try too many untested features at once; hence, we will likely stick with ASIC-resistant proof of work, perhaps with non-Slasher proof of activity as an addon, and look at moving to a more comprehensive proof of stake model over time.

The post Slasher Ghost, and Other Developments in Proof of Stake appeared first on ethereum blog.

ethereum blog

/0 Kommentare/von