One of the issues inherent in many kinds of consensus architectures is that although they can be made to be robust against attackers or collusions up to a certain size, if an attacker gets large enough they are still, fundamentally, exploitable. If attackers in a proof of work system have less than 25% of mining power and everyone else is non-colluding and rational, then we can show that proof of work is secure; however, if an attacker is large enough that they can actually succeed, then the attack costs nothing – and other miners actually have the incentive to go along with the attack. SchellingCoin, as we saw, is vulnerable to a so-called P + epsilon attack in the presence of an attacker willing to commit to bribing a large enough amount, and is itself capturable by a majority-controlling attacker in much the same style as proof of work.
One question that we may want to ask is, can we do better than this? Particularly if a pseudonymous cryptocurrency like Bitcoin succeeds, and arguably even if it does not, there doubtlessly exists some shadowy venture capital industry willing to put up the billions of dollars needed to launch such attacks if they can be sure that they can quickly earn a profit from executing them. Hence, what we would like to have is cryptoeconomic mechanisms that are not just stable, in the sense that there is a large margin of minimum “size” that an attacker needs to have, but also unexploitable – although we can never measure and account for all of the extrinsic ways that one can profit from attacking a protocol, we want to at the very least be sure that the protocol presents no intrinsic profit potential from an attack, and ideally a maximally high intrinsic cost.
For some kinds of protocols, there is such a possibility; for example, with proof of stake we can punish double-signing, and even if a hostile fork succeeds the participants in the fork would still lose their deposits (note that to properly accomplish this we need to add an explicit rule that forks that refuse to include evidence of double-signing for some time are to be considered invalid). Unfortunately, for SchellingCoin-style mechanisms as they currently are, there is no such possibility. There is no way to cryptographically tell the difference between a SchellingCoin instance that votes for the temperature in San Francisco being 4000000000’C because it actually is that hot, and an instance that votes for such a temperature because the attacker committed to bribe people to vote that way. Voting-based DAOs, lacking an equivalent of shareholder regulation, are vulnerable to attacks where 51% of participants collude to take all of the DAO’s assets for themselves. So what can we do?
Between Truth and Lies
One of the key properties that all of these mechanisms have is that they can be described as being objective: the protocol’s operation and consensus can be maintained at all times using solely nodes knowing nothing but the full set of data that has been published and the rules of the protocol itself. There is no additional “external information” (eg. recent block hashes from block explorers, details about specific forking events, knowledge of external facts, reputation, etc) that is required in order to deal with the protocol securely. This is in contrast to what we will describe as subjective mechanisms – mechanisms where external information is required to securely interact with them.
When there exist multiple levels of the cryptoeconomic application stack, each level can be objective or subjective separately: Codius allows for subjectively determined scoring of oracles for smart contract validation on top of objective blockchains (as each individual user must decide for themselves whether or not a particular oracle is trustworthy), and Ripple’s decentralized exchange provides objective execution on top of an ultimately subjective blockchain. In general, however, cryptoeconomic protocols so far tend to try to be objective where possible.
Objectivity has often been hailed as one of the primary features of Bitcoin, and indeed it has many benefits. However, at the same time it is also a curse. The fundamental problem is this: as soon as you try to introduce something extra-cryptoeconomic, whether real-world currency prices, temperatures, events, reputation, or even time, from the outside world into the cryptoeconomic world, you are trying to create a link where before there was absolutely none. To see how this is an issue, consider the following two scenarios:
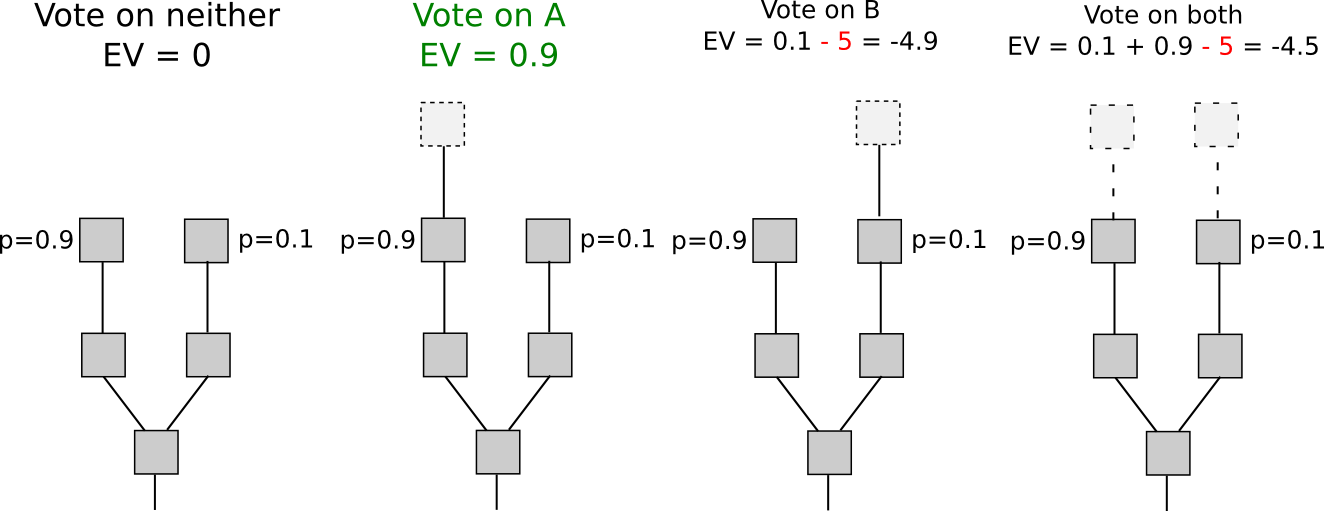
- The truth is B, and most participants are honestly following the standard protocol through which the contract discovers that the truth is B, but 20% are attackers or accepted a bribe.
- The truth is A, but 80% of participants are attackers or accepted a bribe to pretend that the truth is B.
From the point of view of the protocol, the two are completely indistinguishable; between truth and lies, the protocol is precisely symmetrical. Hence, epistemic takeovers (the attacker convincing everyone else that they have convinced everyone else to go along with an attack, potentially flipping an equilibrium at zero cost), P + epsilon attacks, profitable 51% attacks from extremely wealthy actors, etc, all begin to enter the picture. Although one might think at first glance that objective systems, with no reliance on any actor using anything but information supplied through the protocol, are easy to analyze, this panoply of issues reveals that to a large extent the exact opposite is the case: objective protocols are vulnerable to takeovers, and potentially zero-cost takeovers, and standard economics and game theory quite simply have very bad tools for analyzing equilibrium flips. The closest thing that we currently have to a science that actually does try to analyze the hardness of equilibrium flips is chaos theory, and it will be an interesting day when crypto-protocols start to become advertised as “chaos-theoretically guaranteed to protect your grandma’s funds”.
Hence, subjectivity. The power behind subjectivity lies in the fact that concepts like manipulation, takeovers and deceit, not detectable or in some cases even definable in pure cryptography, can be understood by the human community surrounding the protocol just fine. To see how subjectivity may work in action, let us jump straight to an example. The example supplied here will define a new, third, hypothetical form of blockchain or DAO governance, which can be used to complement futarchy and democracy: subjectivocracy. Pure subjectivocracy is defined quite simply:
- If everyone agrees, go with the unanimous decision.
- If there is a disagreement, say between decision A and decision B, split the blockchain/DAO into two forks, where one fork implements decision A and the other implements decision B.
All forks are allowed to exist; it’s left up to the surrounding community to decide which forks they care about. Subjectivocracy is in some sense the ultimate non-coercive form of governance; no one is ever forced to accept a situation where they don’t get their own way, the only catch being that if you have policy preferences that are unpopular then you will end up on a fork where few others are left to interact with you. Perhaps, in some futuristic society where nearly all resources are digital and everything that is material and useful is too-cheap-to-meter, subjectivocracy may become the preferred form of government; but until then the cryptoeconomy seems like a perfect initial use case.
For another example, we can also see how to apply subjectivocracy to SchellingCoin. First, let us define our “objective” version of SchellingCoin for comparison’s sake:
- The SchellingCoin mechanism has an associated sub-currency.
- Anyone has the ability to “join” the mechanism by purchasing units of the currency and placing them as a security deposit. Weight of participation is proportional to the size of the deposit, as usual.
- Anyone has the ability to ask the mechanism a question by paying a fixed fee in that mechanism’s currency.
- For a given question, all voters in the mechanism vote either A or B.
- Everyone who voted with the majority gets a share of the question fee; everyone who voted against the majority gets nothing.
Note that, as mentioned in the post on P + epsilon attacks, there is a refinement by Paul Sztorc under which minority voters lose some of their coins, and the more “contentious” a question becomes the more coins minority voters lose, right up to the point where at a 51/49 split the minority voters lose all their coins to the majority. This substantially raises the bar for a P + epsilon attack. However, raising the bar for us is not quite good enough; here, we are interested in having no exploitability (once again, we formally define “exploitability” as “the protocol provides intrinsic opportunities for profitable attacks”) at all. So, let us see how subjectivity can help. We will elide unchanged details:
- For a given question, all voters in the mechanism vote either A or B.
- If everyone agrees, go with the unanimous decision and reward everyone.
- If there is a disagreement, split the mechanism into two on-chain forks, where one fork acts as if it chose A, rewarding everyone who voted A, and the other fork acts as if it chose B, rewarding everyone who voted B.
Each copy of the mechanism has its own sub-currency, and can be interacted with separately. It is up to the user to decide which one is more worth asking questions to. The theory is that if a split does occur, the fork specifying the correct answer will have increased stake belonging to truth-tellers, the fork specifying the wrong answer will have increased stake belonging to liars, and so users will prefer to ask questions to the fork where truth-tellers have greater influence.
If you look at this closely, you can see that this is really just a clever formalism for a reputation system. All that the system does is essentially record the votes of all participants, allowing each individual user wishing to ask a question to look at the history of each respondent and then from there choose which group of participants to ask. A very mundane, old-fashioned, and seemingly really not even all that cryptoeconomic approach to solving the problem. Now, where do we go from here?
Moving To Practicality
Pure subjectivocracy, as described above, has two large problems. First, in most practical cases, there are simply far too many decisions to make in order for it to be practical for users to decide which fork they want to be on for every single one. In order to prevent massive cognitive load and storage bloat, it is crucial for the set of subjectively-decided decisions to be as small as possible.
Second, if a particular user does not have a strong belief that a particular decision should be answered in one way or another (or, alternatively, does not know what the correct decision is), then that user will have a hard time figuring out which fork to follow. This issue is particularly strong in the context of a category that can be termed “very stupid users” (VSUs) – think not Homer Simpson, but Homer Simpson’s fridge. Examples include internet-of-things/smart property applications (eg. SUVs), other cryptoeconomic mechanisms (eg. Ethereum contracts, separate blockchains, etc), hardware devices controlled by DAOs, independently operating autonomous agents, etc. In short, machines that have (i) no ability to get updated social information, and (ii) no intelligence beyond the ability to follow a pre-specified protocol. VSUs exist, and it would be nice to have some way of dealing with them.
The first problem, surprisingly enough, is essentially isomorphic to another problem that we all know very well: the blockchain scalability problem. The challenge is exactly the same: we want to have the strength equivalent to all users performing a certain kind of validation on a system, but not require that level of effort to actually be performed every time. And in blockchain scalability we have a known solution: try to use weaker approaches, like randomly selected consensus groups, to solve problems by default, only using full validation as a fallback to be used if an alarm has been raised. Here, we will do a similar thing: try to use traditional governance to resolve relatively non-contentious issues, only using subjectivocracy as a sort of fallback and incentivizer-of-last-resort.
So, let us define yet another version of SchellingCoin:
- For a given question, all voters in the mechanism vote either A or B.
- Everyone who voted with the majority gets a share of the question fee (which we will call P); everyone who voted against the majority gets nothing. However, deposits are frozen for one hour after voting ends.
- A user has the ability to put down a very large deposit (say, 50*P) to “raise the alarm” on a particular question that was already voted on – essentially, a bet saying “this was done wrong”. If this happens, then the mechanism splits into two on-chain forks, with one answer chosen on one fork and the other answer chosen on the other fork.
- On the fork where the chosen answer is equal to the original voted answer, the alarm raiser loses the deposit. On the other form, the alarm raiser gets back a reward of 2x the deposit, paid out from incorrect voters’ deposits. Additionally, the rewards for all other answerers are made more extreme: “correct” answerers get 5*P and “incorrect” answerers lose 10*P.
If we make a maximally generous assumption and assume that, in the event of a split, the incorrect fork quickly falls away and becomes ignored, the (partial) payoff matrix starts to look like this (assuming truth is A):
| You vote A | You vote B | You vote against consensus, raise the alarm | |
| Others mainly vote A | P | 0 | -50P – 10P = -60P |
| Others mainly vote A, N >= 1 others raise alarm | 5P | -10P | -10P – (50 / (N + 1)) * P |
| Others mainly vote B | 0 | P | 50P + 5P = 55P |
| Others mainly vote B, N >= 1 others raise alarm | 5P | -10P | 5P + (50 / (N + 1)) * P |
The strategy of voting with the consensus and raising the alarm is clearly self-contradictory and silly, so we will omit it for brevity. We can analyze the payoff matrix using a fairly standard repeated-elimination approach:
- If others mainly vote B, then the greatest incentive is for you to raise the alarm.
- If others mainly vote A, then the greatest incentive is for you to vote A.
- Hence, each individual will never vote B. Hence, we know that everyone will vote A, and so everyone’s incentive is to vote A.
Note that, unlike the SchellingCoin game, there is actually a unique equilibrium here, at least if we assume that subjective resolution works correctly. Hence, by relying on what is essentially game theory on the part of the users instead of the voters, we have managed to avoid the rather nasty set of complications involving multi-equilibrium games and instead have a clearer analysis.
Additionally note that the “raise the alarm by making a bet” protocol differs from other approaches to fallback protocols that have been mentioned in previous articles here in the context of scalability; this new mechanism is superior to and cleaner than those other approaches, and can be applied in scalability theory too.
The Public Function of Markets
Now, let us bring our cars, blockchains and autonomous agents back into the fold. The reason why Bitcoin’s objectivity is so valued is to some extent precisely because the objectivity makes it highly amenable to such applications. Thus, if we want to have a protocol that competes in this regard, we need to have a solution for these “very stupid users” among us as well.
Enter markets. The key insight behind Hayek’s particular brand of libertarianism in the 1940s, and Robin Hanson’s invention of futarchy half a century later, is the idea that markets exist not just to match buyers and sellers, but also to provide a public service of information. A prediction market on a datum (eg. GDP, unemployment, etc) reveals the information of what the market thinks will be value of that datum at some point in the future, and a market on a good or service or token reveals to interested individuals, policymakers and mechanism designers how much the public values that particular good or service or token. Thus, markets can be thought of as a complement to SchellingCoin in that they, like SchellingCoin, are also a window between the digital world and the “real” world – in this case, a window that reveals just how much the real world cares about something.
So, how does this secondary “public function” of markets apply here? In short, the answer is quite simple. Suppose that there exists a SchellingCoin mechanism, of the last type, and after one particular question two forks appear. One fork says that the temperature in San Francisco is 20’C; the other fork says that the temperature is 4000000000’C. As a VSU, what do you see? Well, let’s see what the market sees. On the one hand, you have a fork where the larger share of the internal currency is controlled by truth-tellers. On the other hand, you have a fork where the larger share is controlled by liars. Well, guess which of the two currencies has a higher price on the market…
In cryptoeconomic terms, what happened here? Simply put, the market translated the human intelligence of the intelligent users in what is an ultimately subjective protocol into a pseudo-objective signal that allows the VSUs to join onto the correct fork as well. Note that the protocol itself is not objective; even if the attacker manages to successfully manipulate the market for a brief period of time and massively raise the price of token B, the users are still going to have a higher valuation for token A, and when the manipulator gives up token A will go right back to being the dominant one.
Now, what are the robustness properties of this market against attack? As was brought up in the Hanson/Moldbug debate on futarchy, in the ideal case a market will provide the correct price for a token for as long as the economic weight of the set of honestly participating users exceeds the economic weight of any particular colluding set of attackers. If some attackers bid the price up, an incentive arises for other participants to sell their tokens and for outsiders to come in and short it, in both cases earning an expected profit and at the same time helping to push the price right back down to the correct value. In practice, manipulation pressure does have some effect, but a complete takeover is only possible if the manipulator can outbid everyone else combined. And even if the attacker does succeed, they pay dearly for it, buying up tokens that end up being nearly valueless once the attack ends and the fork with the correct answer reasserts itself as the most valuable fork on the market.
Of course, the above is only a sketch of how quasi-subjective SchellingCoin may work; in reality a number of refinements will be needed to disincentivize asking ambiguous or unethical questions, handling linear and not just binary bets, and optimizing the non-exploitability property. However, if P + epsilon attacks, profit-seeking 51% attacks, or any other kind of attack ever actually do become a problem with objective SchellingCoin mechanisms, the basic model stands ready as a substitute.
Listening to Markets and Proof of Work
Earlier in this post, and in my original post on SchellingCoin, I posited a sort of isomorphism between SchellingCoin and proof of work – in the original post reasoning that because proof of work works so will SchellingCoin, and above that because SchellingCoin is problematic so is proof of work. Here, let us expand on this isomorphism further in a third direction: if SchellingCoin can be saved through subjectivity, then perhaps so can proof of work.
The key argument is this: proof of work, at the core, can be seen in two different ways. One way of seeing proof of work is as a SchellingCoin contest, an objective protocol where the participants that vote with the majority get rewarded 25 BTC and everyone else gets nothing. The other approach, however, is to see proof of work as a sort of constant ongoing “market” between a token and a resource that can be measured purely objectively: computational power. Proof of work is an infinite opportunity to trade computational power for currency, and the more interest there is in acquiring units in a currency the more work will be done on its blockchain. “Listening” to this market consists simply of verifying and computing the total quantity of work.
Seeing the description in the previous section of how our updated version of SchellingCoin might work, you may have been inclined to propose a similar approach for cryptocurrency, where if a cryptocurrency gets forked one can see the price of both forks on an exchange, and if the exchange prices one fork much more highly that implies that that fork is legitimate. However, such an approach has a problem: determining the validity of a crypto-fiat exchange is subjective, and so the problem is beyond the reach of a VSU. But with proof of work as our “exchange”, we can actually get much further.
Here is the equivalence: exponential subjective scoring. In ESS, the “score” that a client attaches to a fork depends not just on the total work done on the fork, but also on the time at which the fork appeared; forks that come later are explicitly penalized. Hence, the set of always-online users can see that a given fork came later, and therefore that it is a hostile attack, and so they will refuse to mine on it even if its proof of work chain grows to have much more total work done on it. Their incentive to do this is simple: they expect that eventually the attacker will give up, and so they will continue mining and eventually overtake the attacker, making their fork the universally accepted longest one again; hence, mining on the original fork has an expected value of 25 BTC and mining on the attacking fork has an expected value of zero.
VSUs that are not online at the time of a fork will simply look at the total proof of work done; this strategy is equivalent to the “listen to the child with the higher price” approach in our version of SchellingCoin. During an attack, such VSUs may of course temporarily be tricked, but eventually the original fork will win and so the attacker will have massively paid for the treachery. Hence, the subjectivity once again makes the mechanism less exploitable.
Conclusion
Altogether, what we see is that subjectivity, far from being an enemy of rigorous analysis, in fact makes many kinds of game-theoretic analysis of cryptoeconomic protocols substantially easier. However, if this kind of subjective algorithm design becomes accepted as the most secure approach, it has far-reaching consequences. First of all, Bitcoin maximalism, or any kind of single-cryptocurrency maximalism generally, cannot survive. Subjective algorithm design inherently requires a kind of loose coupling, where the higher-level mechanism does not actually control anything of value belonging to a lower-level protocol; this condition is necessary in order to allow higher-level mechanism instances to copy themselves.
In fact, in order for the VSU protocol to work, every mechanism would need to contain its own currency which would rise and fall with its perceived utility, and so thousands or even millions of “coins” would need to exist. On the other hand, it may well be possible to enumerate a very specific number of mechanisms that actually need to be subjective – perhaps, basic consensus on block data availability validation and timestamping and consensus on facts, and everything else can be built objectively on top. As is often the case, we have not even begun to see substantial actual attacks take place, and so it may well be over a decade until anything close to a final judgement needs to be made.
The post The Subjectivity / Exploitability Tradeoff appeared first on .